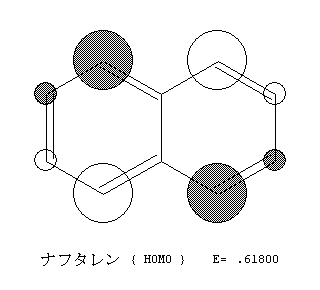
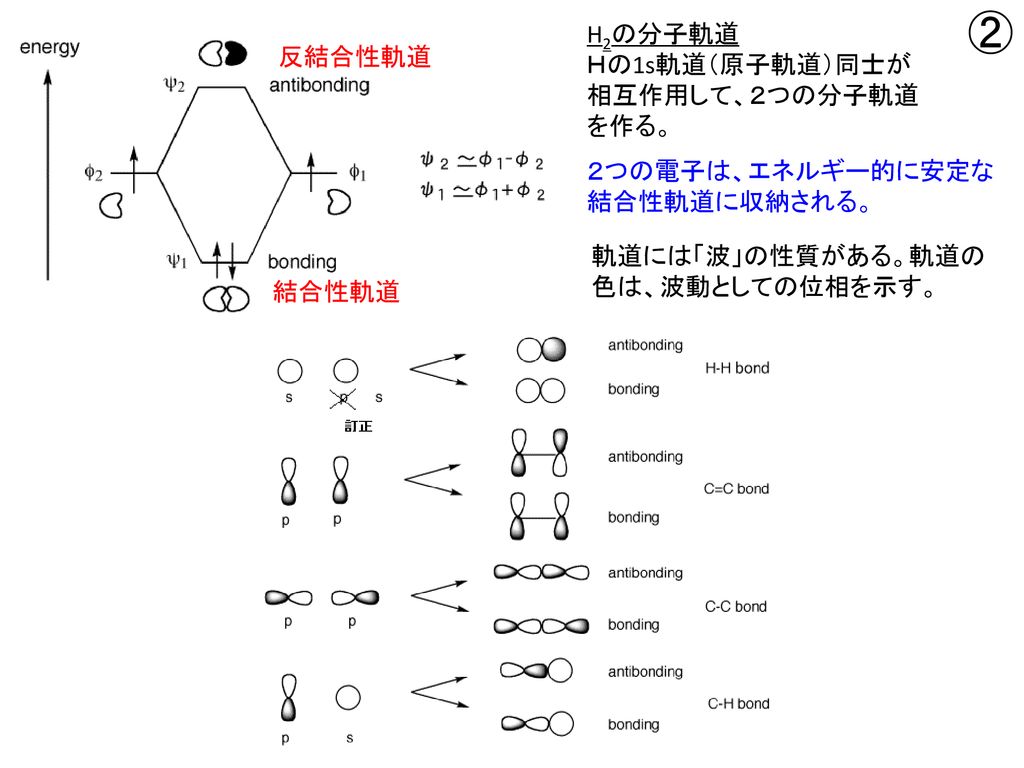
例 表31 点群とそれに属する分子 点群の名称 群 元 素 この群に属する分子 h 2o, so 2, シスブタジエン 1,2ジクロロエチレン(シ ス) nh3, pcl3, ch3cl co, hcl トランス‐ブタジエン 1,2ジクロロエチレン(トランス) ナフタレン, アントラセン, ピレン, ピセン ベンゼン,がいたが、これは2pz 軌道で、分子面に垂直にでているよ。この軌道が横の2pz 軌道と重なって分子全体 で一つの分子軌道を形成するんだが、これをπ電子軌道と呼んでいる。このπ電子軌道の中には電子(π電 子) が合計6 個存在することになる。ここまではいいかい? • アリス:化学構造式のブタジエンの π 分子軌道 Huckel 近似が示唆する分子の性質 ブタジエンでの結果を検討しよう。 表示される固有値 X が大きい程、軌道エネルギーは低い。 エネルギーの高い軌道ほど 2Pz 軌道の係数の正負の反転が頻繁、 つまり波動関数に節が多くあることがわかる。 各炭素原子の 2Pz 原子軌道

水の分子軌道について 水の分子軌道の形状についての質問させていただきます Okwave
ブタジエン 分子軌道
ブタジエン 分子軌道-M ) * 9 % "&'!係数である。この軌道が次式の分子軌道の方程式を満たすものとする。 ˆ ( 1,2,3, ) F i i i i (2) 軌道エネルギーは次式となる。 ˆ i i i i i F dv dv (3) iは実数であるとして複素共役の記号*は付けていない。{ i}が相互に規格直交すれば、即ち、 1( ) i k ik 0 ( ) i k dv i k ならば(3)式の分母は不要であるが




A A A A C A A A Aœa A
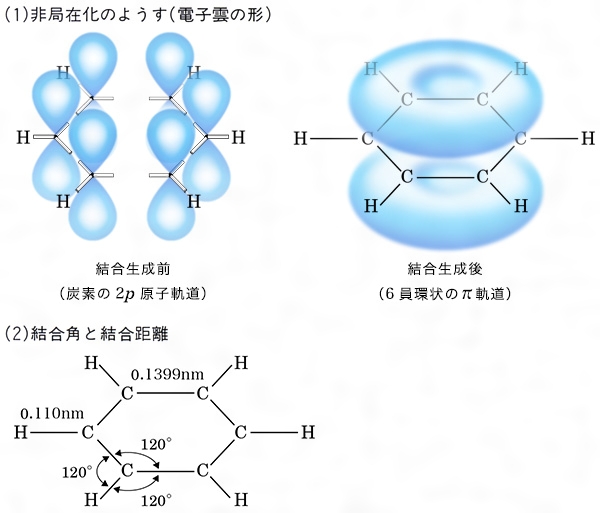
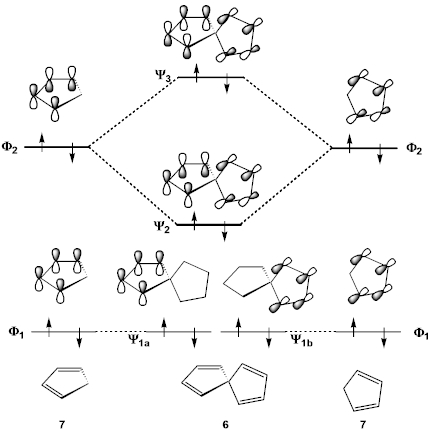
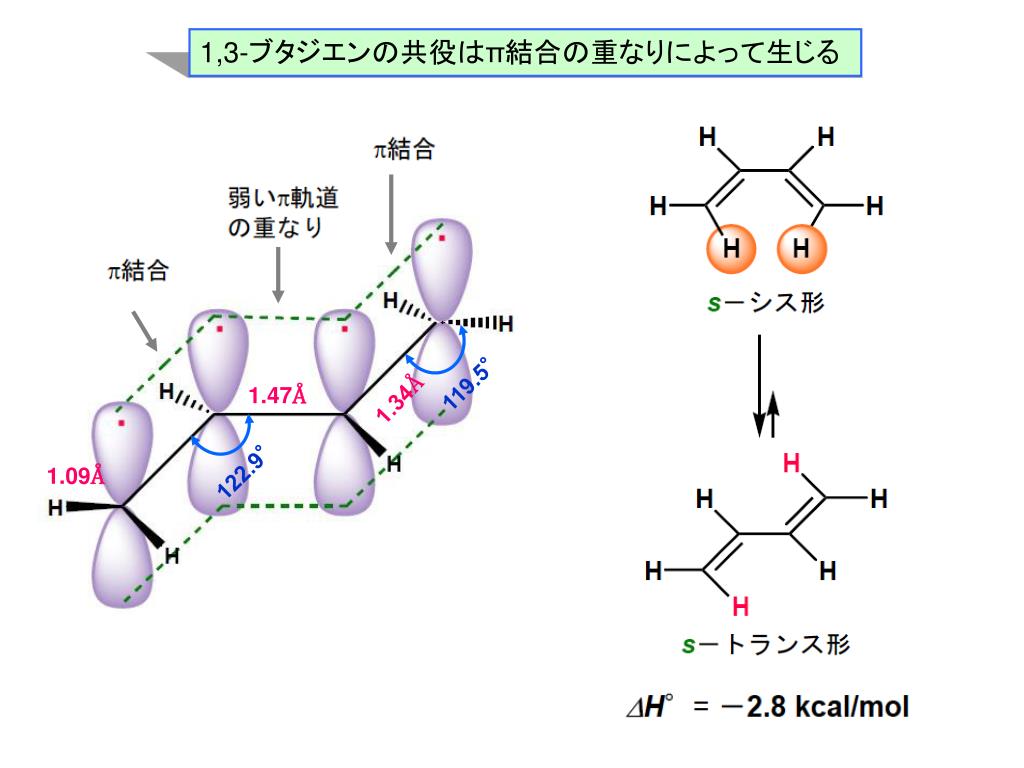
P原子軌道 ブタジエンは図 3 にあるような分子で、 6 つの水素 1s 軌道と炭素原子の(1s 軌道 H C は考えないとして)2s、2px、2py 軌道各 2 H s原子軌道 個が分子面内にあるが、これらの原子軌 道から出来るs分子軌道は深いエネルギ H 図3 C C H H C H ブタジエンの 2pZ 原子軌道 ー準位にあるとして原子軌道同士の重なり 結合 ss 結合,p xp x 結合 共有結合軸方向に沿って形成 結合軸回りに回転可能 結合 二つのp軌道が互いに平行に接する 共有結合軸方向に垂直方向に形成 結合軸方向に回転不能( 結合が切断) 混成軌道 sp3混成 1本のs軌道と3本のp軌道から 結合を形成 正四面体,結合角109ブタジエンシクロブテンの軌道相関図。熱過程許容は右側になると判断。 B 6電子系の電子環状反応 (1) MO準位を6つずつ描いて、A のように軌道相関図を作成する(図4)。遷移状態として逆旋側に Hückel縮重を、同旋側にMöbius縮重を挟む(図1参照)。分子軌道の位相を重ね書きしてみると
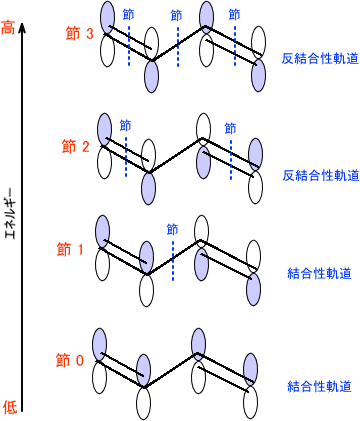
シクロブタジエンの分子軌道(筆者作成) e=αの軌道が縮退しているため、基底状態が三重項となります。 ここで全電子エネルギーに注目すると、エチレン二分子の値よりも も不安定化する結果となっています。そのため、シクロブタジエンは安定に存在できない反芳香族性を有する分子子軌道は結合性分子軌道,逆 の場合は反結合性分子軌道 となる。ブタジエンのψ1,ψ2は結合性分子軌道であ り,ψ3,ψ4は反結合性分子軌道である。 一般にn個 の炭素原子からなる共役ポリエンでは, n個 の分子軌道関数ができ,エ ネルギーの低い方から順 にψ1,ψ2分子の面に垂直な軌道となっている。π電子の結合 はσ結合に比べ弱くエネルギー準位が深くないために隣の原子へ自由に飛び移る。 ヒュッケル法(Huc kel method) 分子の波動関数を = c1ϕ1 c2ϕ2 c3ϕ3 c4ϕ4 (1) 異なるπ軌道の重なり積分を0とする。(ϕk;ϕ ′ k) = kK′,
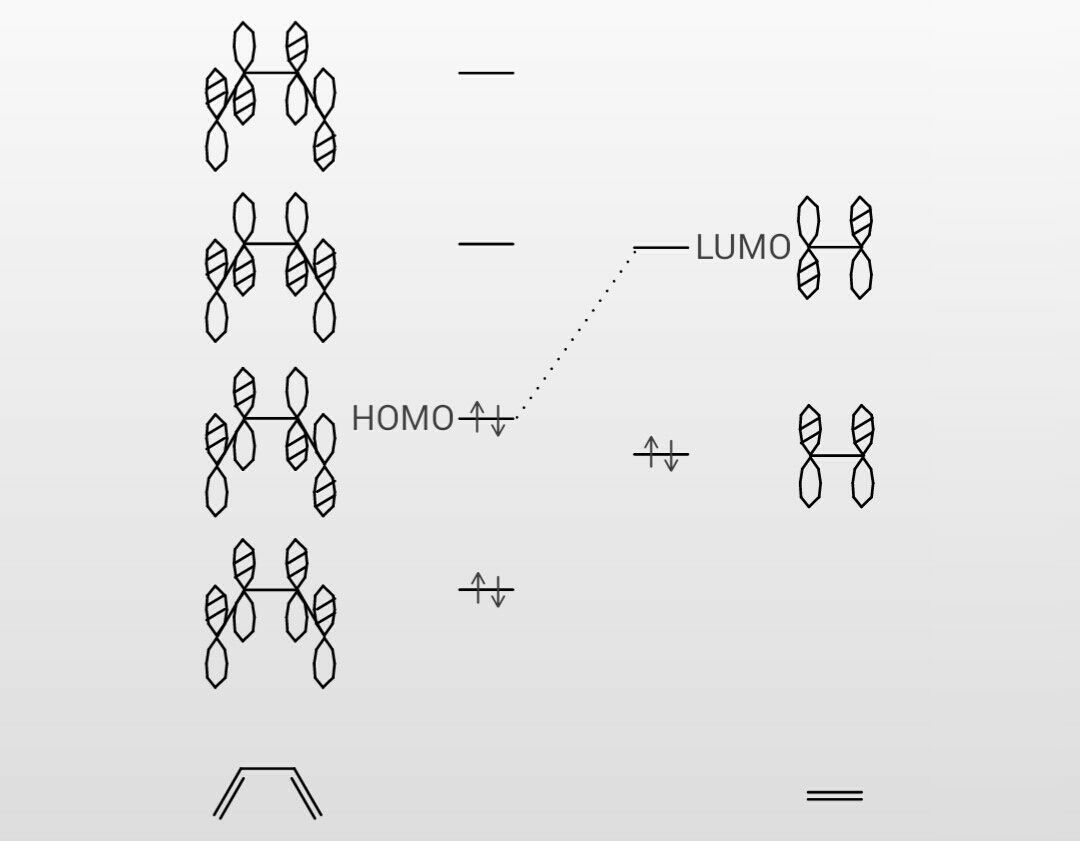
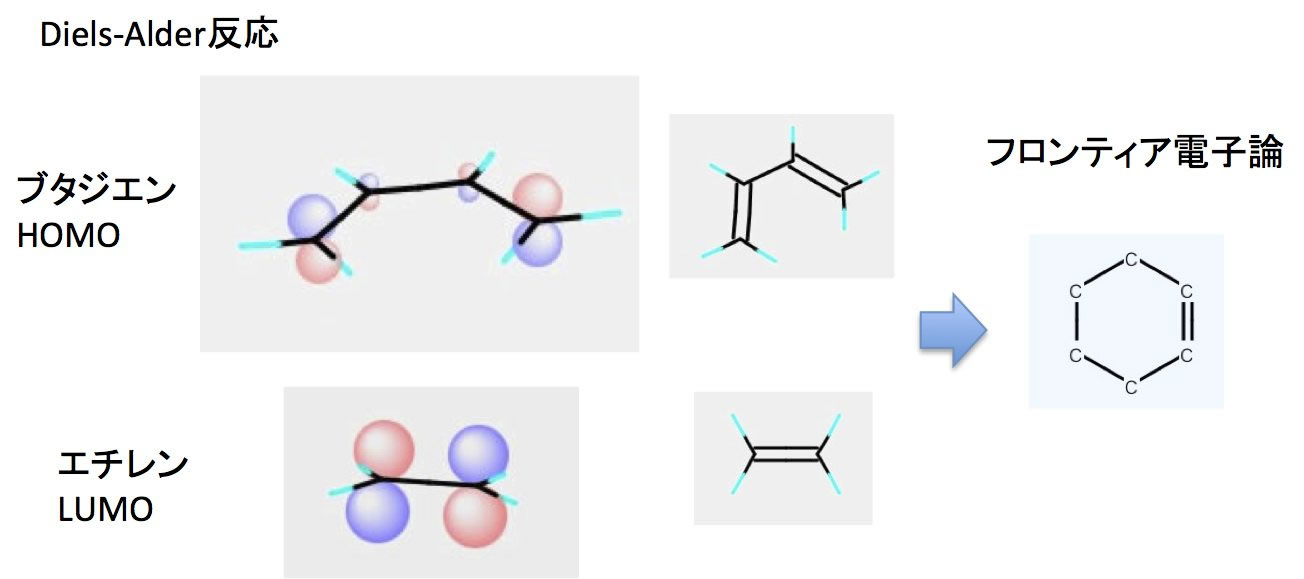
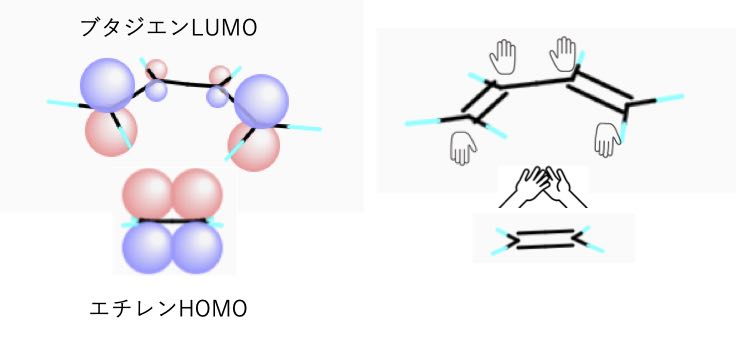
1,3ブタジエン (4π電子) エテン (2π電子) シクロヘキセン (環化付加物) DielsAlder反応は42環化付加反応である! 4つのπ電子を持つ共役した4つの原子の集団が, 2つのπ電子を持つ二重結合と反応する. 通常、ジエンに電子供与基(EDG)、ジエノファイルには電子吸引基(EWG) を持ブタジエンのπ分子軌道 E H 反結合性 H H H 反結合性 H H H H 分子軌道 H H H H H H H H H H 結合性 分軌道 H H H H 分子軌道 H H 練習問題(2Z,4Z)2,4hexadieneは、 131,3btdibutadieneと比べてと比べて 、sシス形配座のシス形配座の 割合が極めて低い。その理由は何か? 2つのメチル基の間の立体障害が大きい ため単結合と2重結合が交互につながっている共役分子を考え、分子面に垂直な炭 素の2Pz軌道だけからなるπオービタルのみを考える。その場合、波動関数Ψ はLCAOで表すと エチレン Ψ=c AA c BB ブタジエン Ψ=c AA c BB c CC c DD 永年行列式の規模が大きくなると計算するのが煩雑になるので



Iqce Jp




ヒュッケル法 前編 手計算で分子軌道を求めてみた Chem Station ケムステ
Hückel (ヒュッケル) 法の要点 π 電子を提供する炭素原子の数を N とする (例 エチレン C 2 H 4 は N = 2, ブタジエン C 4 H 6 は N = 4, ベンゼン C 6 H 6 は N = 6) ハミルトニアン行列 H は N × N 対称行列 対角要素は全て α とおく i j, j i ( i ≠ j) 非対角要素は, 炭素 i, j分子には多くの軌道 *(原子軌道1 ,分子軌道)があると考え る。分子のエネルギーが最も低い状態(基底状態)では,電 子はエネルギーの低い軌道から順に2個ずつ入る(図1)。 電子に占められているエネルギーの最も高い分子軌道を最 高被占分子軌道図4.1,3ブタジエンとジエンの軌道相互作用 図5.dieneとdienophileのエネルギー相関図 2.DielsAlder反応 フロンティア軌道を用いた反応予測は芳香族の置換反応 のみでなく、DielsAlder反応のような2分子間の軌道の位 相の関係する反応に対しても有効である。DielsAlder反応 とはジエン(diene)と求ジエン



かがくののおと



Misaki Lab Jp
ヒュッケル法で求めたブタジエンの分子軌道について、 trans ブタジエンを例に対称性から考察してみる。 trans ブタジエンではC 2 軸、i, σ h を持ち、C 2h 点群に属する。 (1) ヒュッケル法で得られた4 つの分子軌道は安定な方から節の数が0,1,2,3 となっていることをヒ ントにして、その概形Eπ(ブタジエン)-2×eπ(エチレン)=4α4β2(2α2β) =0 つまり,シクロブタジエンでは非局在化安定化エネルギーはゼロである. 占有数 分子軌道係数 計算出力例 lcaomoの係数(分子軌道係数)を求めるには,永年行列式を解いてトランスブタジエンのπ""π* 遷移 点群は? 各軌道の既約表現は? x, y, z"偏光に対して,どの遷移が許容か? (前回の授業




書籍紹介 分子軌道法 Pod版 廣田 穰 著 化学



ディールスアルダー反応 この世を科学的に知ろう
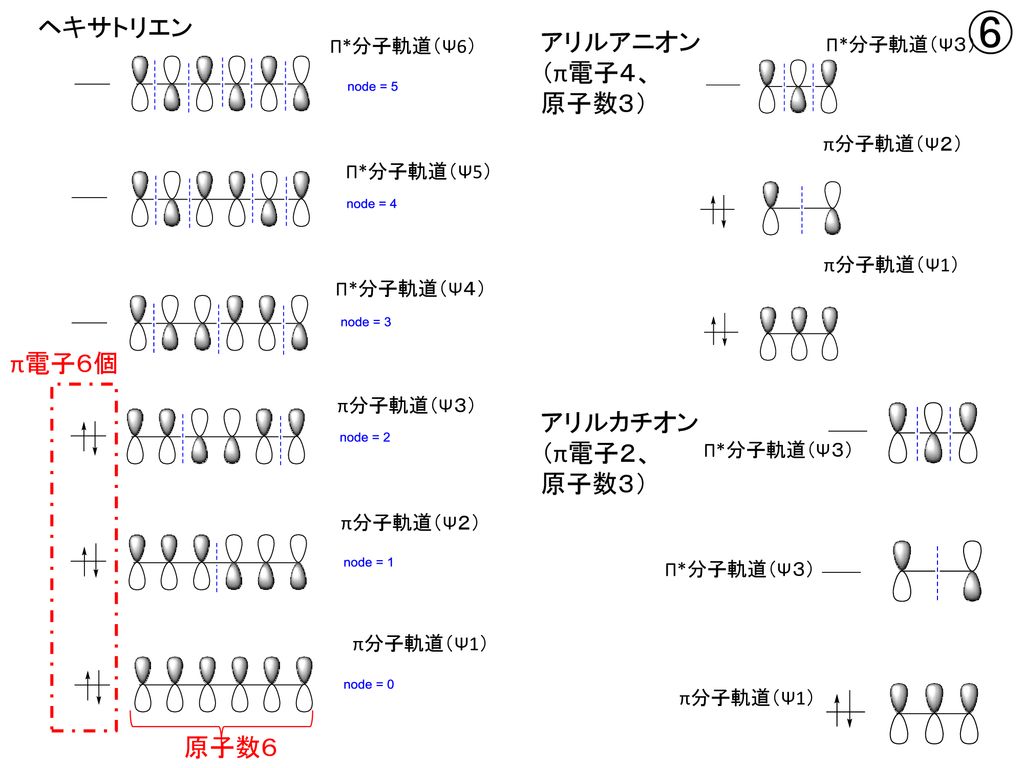
I2) ヒュッケル分子軌道沵を用いて,H 3 がより安定なのは直線状態と三角形状態の どちらであるか決定せよ。H 3, H 3 –ではどうか。 x =(α−E) βとおくと、直線状態、三角形状態の軌道エネルギーは 直線状態 α β αβ α β 2 2 2 0 0 1 1 1 1 0 3 2 1 3 = − = − = = − = ∴ E E E x x x x x 三角形状態 αβ αβ 電子が入っていない(空の)最もエネルギーが低い軌道はπ*軌道になります。 つまり、エチレンの場合は、HOMO=π軌道、LUMO=π*軌道となります。 エチレンの HOMOとLUMOはこのように簡単に求めることができます。 しかし、π電子の数が増えていくとπ軌道の数新しい分子軌道を3つ作る 4 p軌道の相互作用:軸が平行であることが必要 軸が平行 5 演習問題アリルカチオンの以下の2つの配座異性体は どちらが安定か。 c cc h h h h h c cc h h h h h 6 アリルカチオンのπ分子軌道:エネルギー図 エネルギー c 2pz c c c h h h h h 1 2 3 7 アリルカチオンの安定



Ch3 の分子軌道の構築



Quantum Huckel Approximation
図241 1,3–ブタジエンとエテンの42付加環化反応における HOMO–LUMO相互作用 エテンと1,3–ブタジエンの分子軌道は図314と図52を参照すること. ほとんどのDiels–Alder 反応のジエノフィルは少なくとも一つ電子求引基をもってでは「結合性軌道・反結合性軌道とは何か」であるが、その名の通り結合性軌道は分子 1,3ブタジエンの軌道を示している下の図で青色で囲んでいる軌道がHOMOとなっている。 それに対し、LUMOは「Lowest Unoccupied Molecular Orbital」のことであり、最低空軌道と訳される。LUMOは電子がない空の軌道の∫ 12d < ∫ 2 2d < ∫ m 2d < 1 m 2;



芳香族化合物とは コトバンク




Wo16 号 有機エレクトロルミネッセンス素子 表示装置 照明装置 蛍光発光性化合物及び発光性薄膜 Astamuse
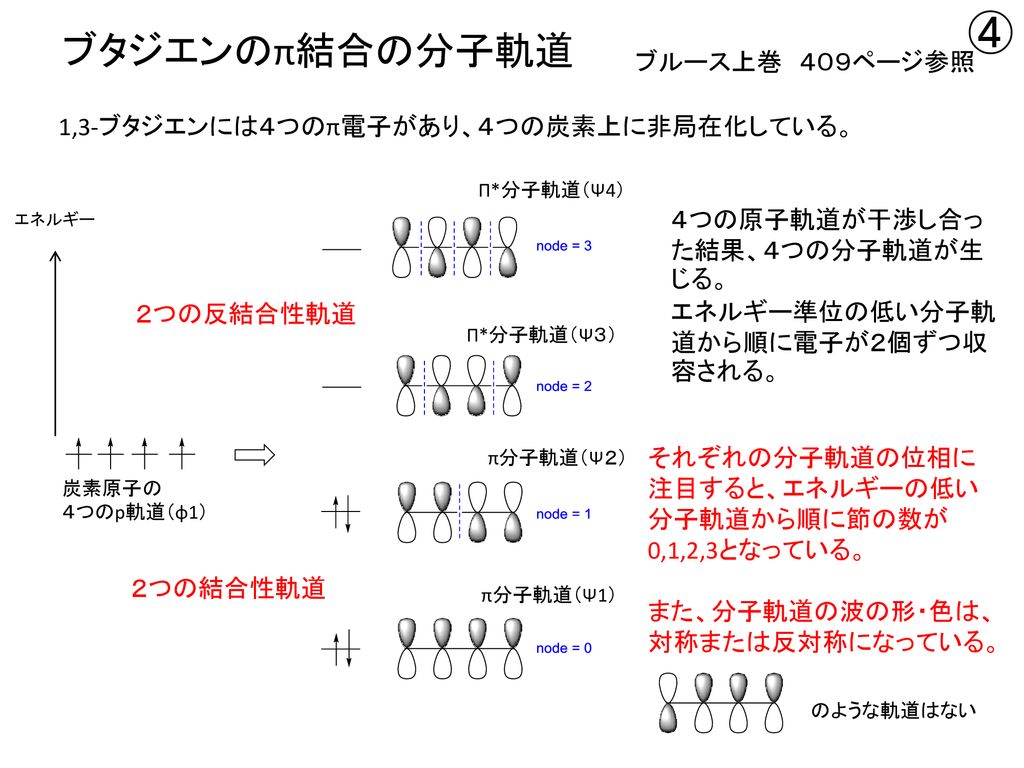
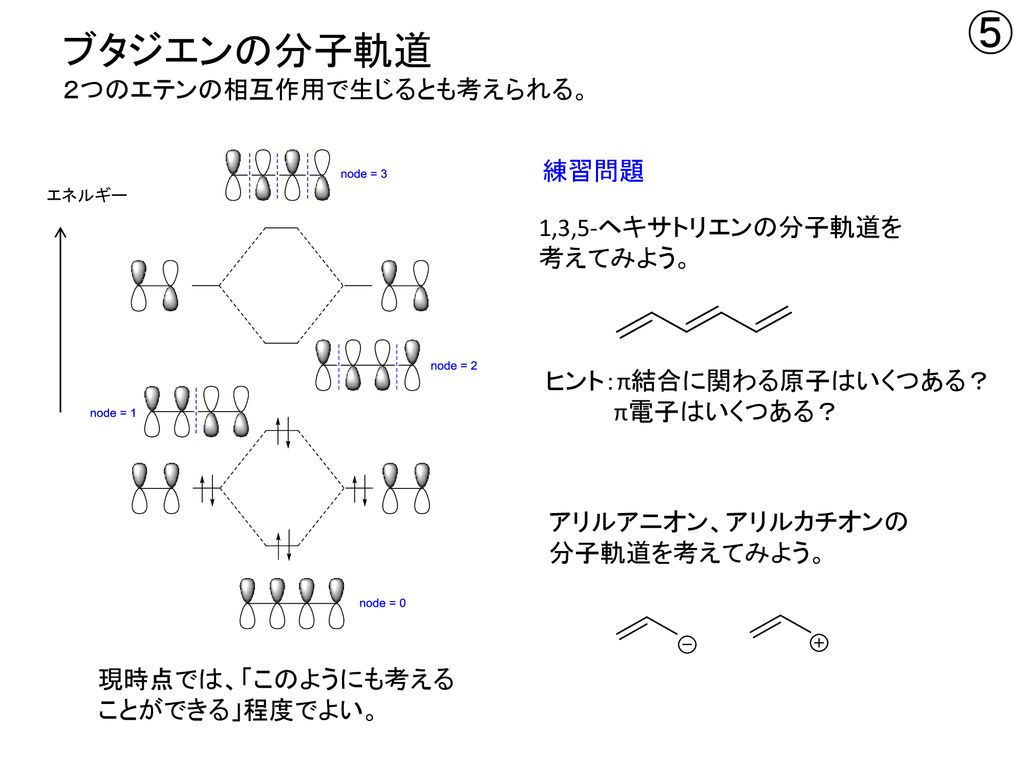
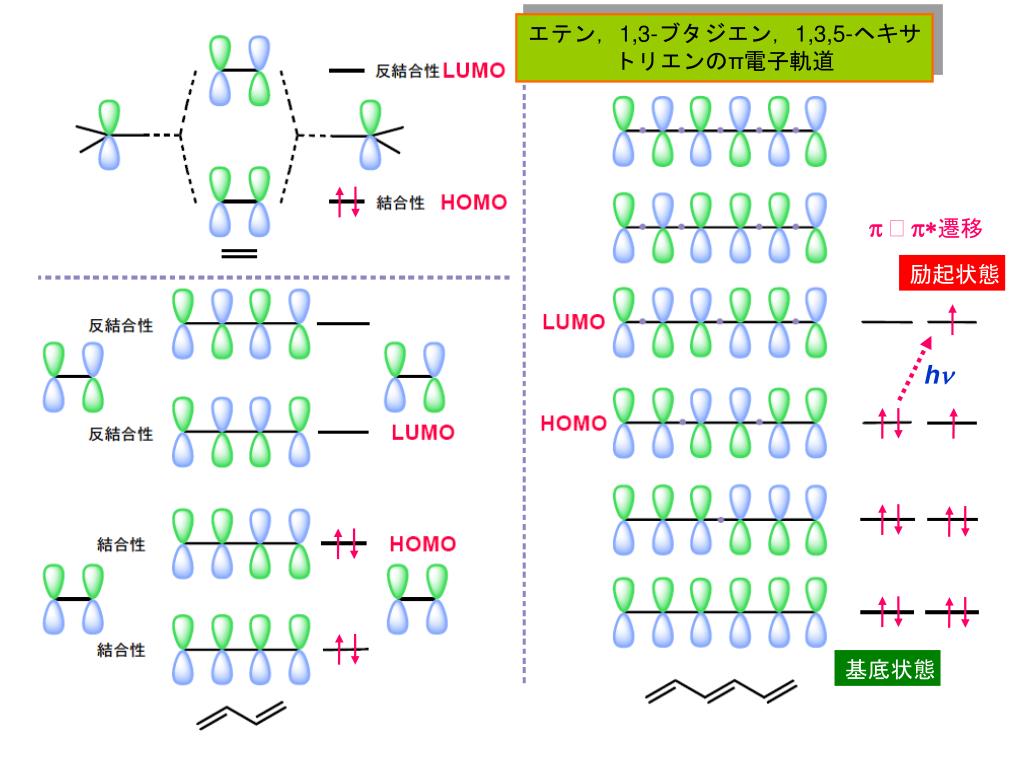
ブタジエンは、共役二重結合を持つ最も単純な分子である。 1,3ブタジエンのπ分子軌道についても、C1~C4の2p z軌道がすべて相互作用して、 新しい分子軌道を4つ作ると考える。分子軌道の形とエネルギーは、下の図のようにな あることがわかっている。よってシクロブタジエンの全エネ ルギーはエチレン1 分子の全エネルギーのちょうど2 倍であるから、シクロブタジエンと2 つの 孤立したエチレン分子の安定性は等しい。 i3 ヒュッケル分子軌道法を用いて,トリメチレンメタンのs 電子全エネルギーを求めブタジエン: E π = 2 e 1 2 e 2 = 2(a 162 b) 2(a 062 b) = 4 a 448 b より、 E π (ブタジエン) - 2 E π (エチレン) = –048 b :非局在化による安定化 1プロペン (CH 2 =CH–C • H 2) の π分子軌道 3個の π軌道からなる系に相当。 連立方程式 (414) は次のようになる



分子軌道法計算 hmo法2 1



分子軌道の書き方が全く分かりません このn2とo2の分子軌道がど Yahoo 知恵袋
ブタジエンはπ電子が4つあるのに、なぜ1の状態をとるときに横に書くスピンは2つなんですか? また、基底状態のときは、1と2の両方の状態をとるということですか? 教えてください! 1 回答 ベストアンサー 黒龍 2年以上前 π電子によって2つの結合性軌道と2) " &( * ) ,&#$& *%9 ( & /58 ∫ 1H 1d ∫ 2H 2d ∫ mH md 2pブタジエン分子の基底状態 分子軌道の模式図 最低励起エネルギーはψ 3 ←ψ 2 の電子遷移によるから ∆ E = α– 0618β– α– 0618β= – 1236β



Misaki Lab Jp




Pdfファイル
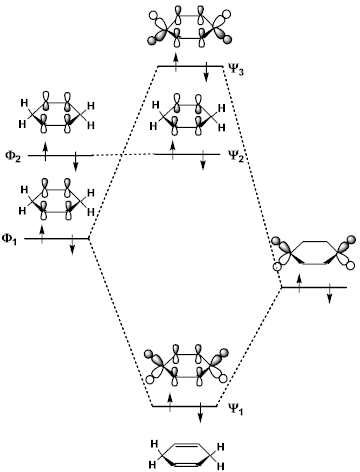
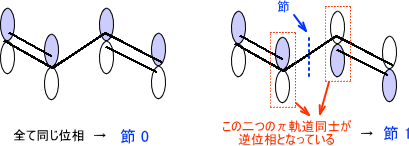
図4 ブタジエンのp分子軌道 エネルギー (1 5)b 2 1 ( 1 5)b 2 1 (1 5)b 2 1(1 5)b 2 1 p分子軌道 4 もなって低くなっていることに対応している。 例題 アリルラジカルの分子軌道をヒュッケル法で 求めるには、(9)式で3×3 行列式を解けばよい。 0 0 0 =E E E b a b a b a b これを解いて、分子軌道エチレンとブタジエンの軌道間相互作用が問題になるが、まずは、それぞれの分子軌道の形とエネルギ ー準位を知る必要がある。エチレンの分子軌道は、2組のメ チレン ch 2 の分子軌道から組み立てることができる(参考 書:大野公一、量子化学、岩波書店、 1996 年)。前回学んだ ah 2 型 ブタジエンの分子軌道についてなんですが、ウォーレンの教科書には画像のように書いてあります。 ですが、一番上の(エネルギーの高い)軌道は節面が3つできるように全ての隣り合う位相は逆にな るのではないでしょうか? のように節面が二つで左右非対称の形で書いてあ



Iqce Jp



3
==ヒュッケルの分子軌道計算プログラム== by KENZOU (0505) ==== Molecular Orbital Calculation program ==== In1= 1.エネルギー縮退のない分子 ブタジエン アリルラジカル ビシクロブタジエン ビシクロヘキサジエン スチレン ナフタレンブタジエンの分子軌道 ブタジエンになると、p軌道が4つになり電子も4つになります。p軌道の方向で組み合わせを考えると4種類あることがわかります。下の青の軌道( π1、π2)は、少なくとも2つの軌道が重なりますが、上の赤い軌道(π * 3、π * 4)では、重なりが無く不安定だということがシクロブタジエン C4H4 上の図のように分子軸を取り番号付けをする。 永年行列式は次のようになる。 x 1 0 1 1 x 1 0 0 1 x 1 1 0 1 x = 0 永年方程式は x (x 3 – 2x) – x 2 – x 2 = x 2 (x 2 – 4 ) = 0 より x = 0, ±2 を得る。 エネルギーの低い順に分子軌道を求めよう。 x



Www2 Meijo U Ac Jp




水の分子軌道について 水の分子軌道の形状についての質問させていただきます Okwave
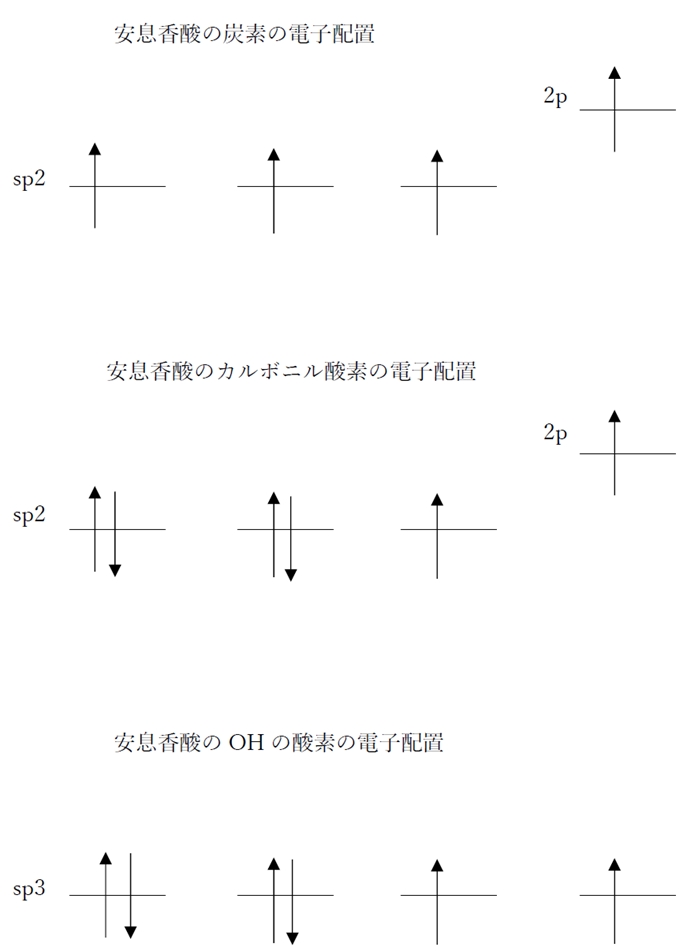
ブタジエン( ch2=chch=ch2 ) 本来,電子の運動は,分子全体に広がっている.エネルギーを詳しく議論するには,分子軌道で議論しなければならないが,分子の形や大まかな性質を考える場合には,混成軌道の考えかたのほうが簡単である.11章分子構造 分子軌道法 Eπ(ブタジエン)-2 ×Eπ(エチレン)=4α4β2(2α2β) =0 つまり,シクロブタジエンでは非局在化安定化エネルギーはゼロである. 占有数 9 Electron Population on atom atom Population 1 2 3 4 BondOrder Matrix 21 31 32 41 42 43 05.分子軌道法への応用 まず通常の量子力学における分子軌道法に従い、シクロブタジエン分子の分子軌道を導 出してみよう。まず分子全体の波動関数を個々の原子の波動関数の線形結合にて、 ψ=cc1ϕ1 22ϕc3ϕ3c44ϕ と表現する。 (,) (,) (,) ϕ ϕ''δ ϕϕα ϕϕ kk




反結合性軌道 Youtube
%E3%81%AE%E7%B5%90%E5%90%88%E3%81%AB%E3%81%AF%CF%83%E7%B5%90%E5%90%88%E3%81%8C1%E3%81%A4%E5%90%AB%E3%81%BE%E3%82%8C%E3%82%8B%E3%80%82.jpg)



86回薬剤師国家試験問5 L 3ブタジエンの原子は同一平面上
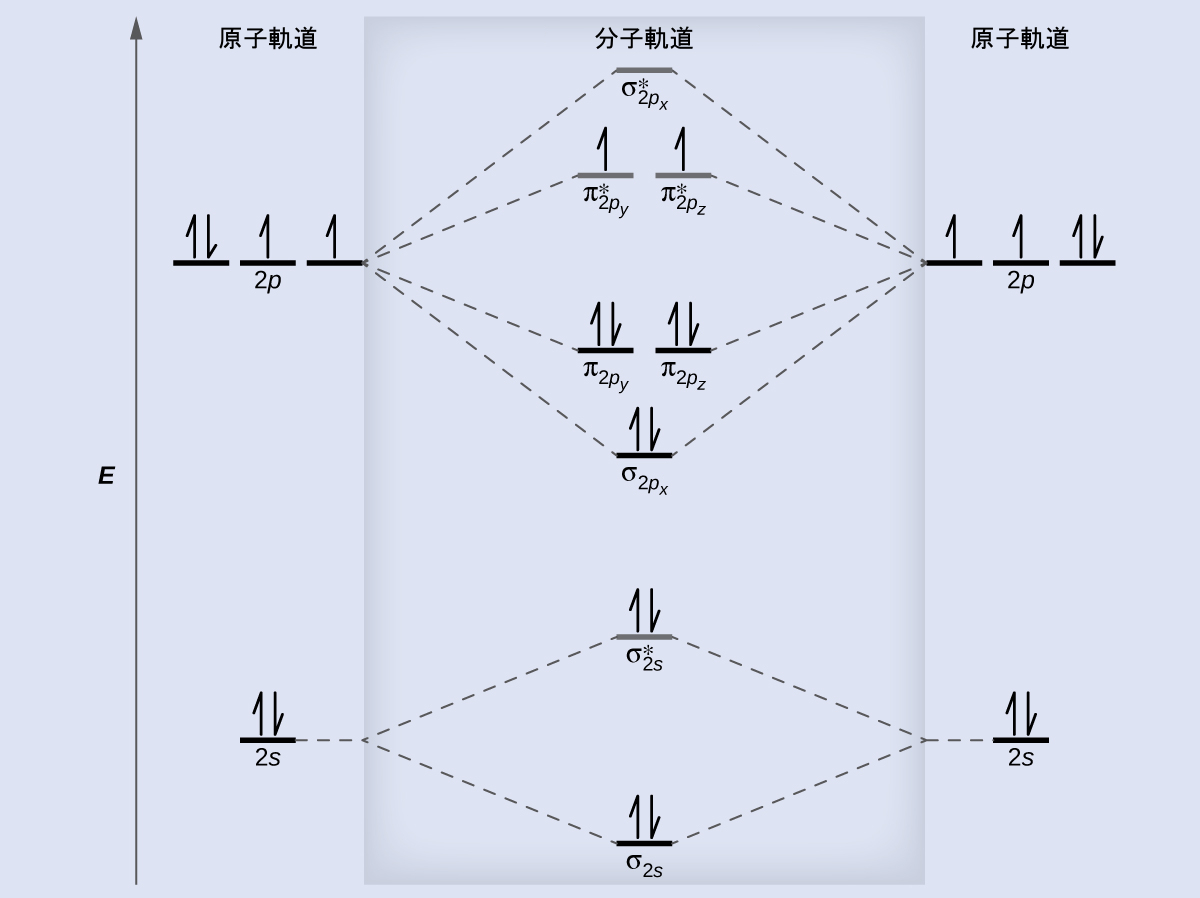
そこで,群論使って軌道の対称性から電子遷移 の可否を偏光も含めて考える。 エチレンの π$$π* 遷移$ 点群はD 2h x y z x y z π π* 点群D 2hの対称要素は何があるか? (クイズ) 制限時間5分 点群D 2hの対称要素は何があるか? (クイズ) 制限時間?分 E C 2 z C 2 y C 2 x i




ヒュッケルの分子軌道法計算プログラム ヒュッケルの分子軌道法 この言葉は小生にとって大変懐かしい言葉です 初めて耳にした学生時代 ヒュッケル と言う音声にしゃっくりの様な 何か面白みと親しみを感じ また 量子力学のややこしい計算に




バイオ研究者がもっと知っておきたい化学1 化学結合でみえてくる分子の性質 羊土社



有機化学者のための分子軌道法



Chem S U Tokyo Ac Jp




Homo Lumoの概念 結合性軌道 反結合性軌道のエネルギーの違い リョースケ大学




ブタジエンはp電子が4つあるのに なぜ1の状態をとるときに横に書くスピンは2 Clearnote



1



分子軌道理論 Molecular Orbital Theory Mo理論 Ppt Download



2 7 より複雑な分子へ スペクトル色々




第5回



86回薬剤師国家試験問5 L 3ブタジエンの原子は同一平面上



Note



T Soka Ac Jp



第8章 共有結合の高度な理論 化学 第2版



Acbio2 Acbio U Fukui Ac Jp



Acbio2 Acbio U Fukui Ac Jp




ヒュッケル法 前編 手計算で分子軌道を求めてみた Chem Station ケムステ



分子軌道理論 Molecular Orbital Theory Mo理論 Ppt Download



共同発表 有機分子ワイヤを通る電子移動速度の高速化を実現 電子移動研究 分子デバイスの新たなマイルストーン



ブタジエンの分子軌道についてなんですが ウォーレンの教科書には画像 Yahoo 知恵袋



キリヤ Q A




量子力学特論 レポート課題4 17 6 2 Inftyproject Liner Combination Of Atomic Orbital 分子軌道法 シュレディンガ 方程式の Inftyproject 左から Inftyproject をかけて積分を行う Inftyproject よって Inftyproject と書き直せる 但し Inftyproject は全積分
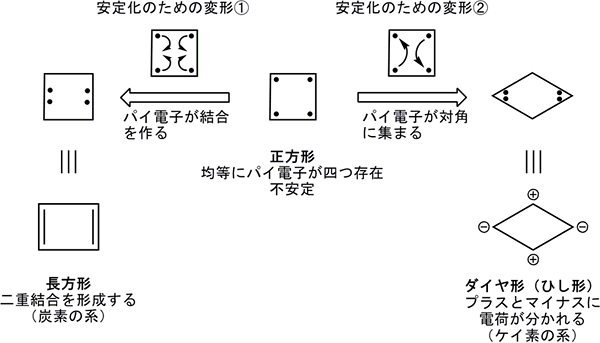



4つのケイ素で ひし形 の新環状化合物を初合成 理化学研究所



量子力学野郎 Ryoshipower Twitter



プロセス合理化 反応時間の短縮
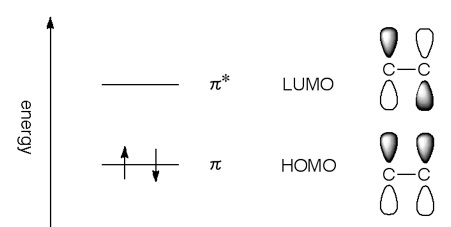



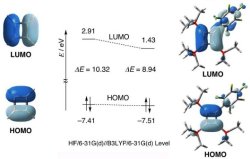
Homoとlumo



分子軌道理論 Molecular Orbital Theory Mo理論 Ppt Download



芳香族化合物とは コトバンク



キリヤ Q A



デジタル分子模型で見る化学結合 6 フロンティア分子軌道から 作られる直前の化学結合の様子を見る事ができる



Misaki Lab Jp



2 7 より複雑な分子へ スペクトル色々



有機反応機構 芳香族求電子置換反応



Chem Tohoku Ac Jp



Acbio2 Acbio U Fukui Ac Jp




物理系薬学演習 第1回 演習問題 Flashcards Quizlet



Document




16 共役p電子系 単純 Huckel 法



3



有機化学者のための分子軌道法



Misaki Lab Jp




最も低いエネルギー分子軌道 Pi1 はそうするだけでした そして 1つが3つのブタジエン分子軌道でした Png 無料ダウンロード Key0



分子軌道理論 Molecular Orbital Theory Mo理論 Ppt Download




1 3 ブタジエンのp軌道の分子軌道の質問です 光過程による環化反応は 化学 教えて Goo



結合性軌道と反結合性軌道 Homoとlumo




シクロブタジエン Wikipedia




日曜化学 3 分子軌道法と可視化 Python Matplotlib Tsujimotterのノートブック



筑波大 頑丈極まりないベンゼン環を常圧 1 で開裂させる反応を発見 Tech




有機分子の分子軌道計算と活用 分子軌道法を用いた有機分子の性質と基本的反応の計算と活用 染川 賢一 本 通販 Amazon




第5回
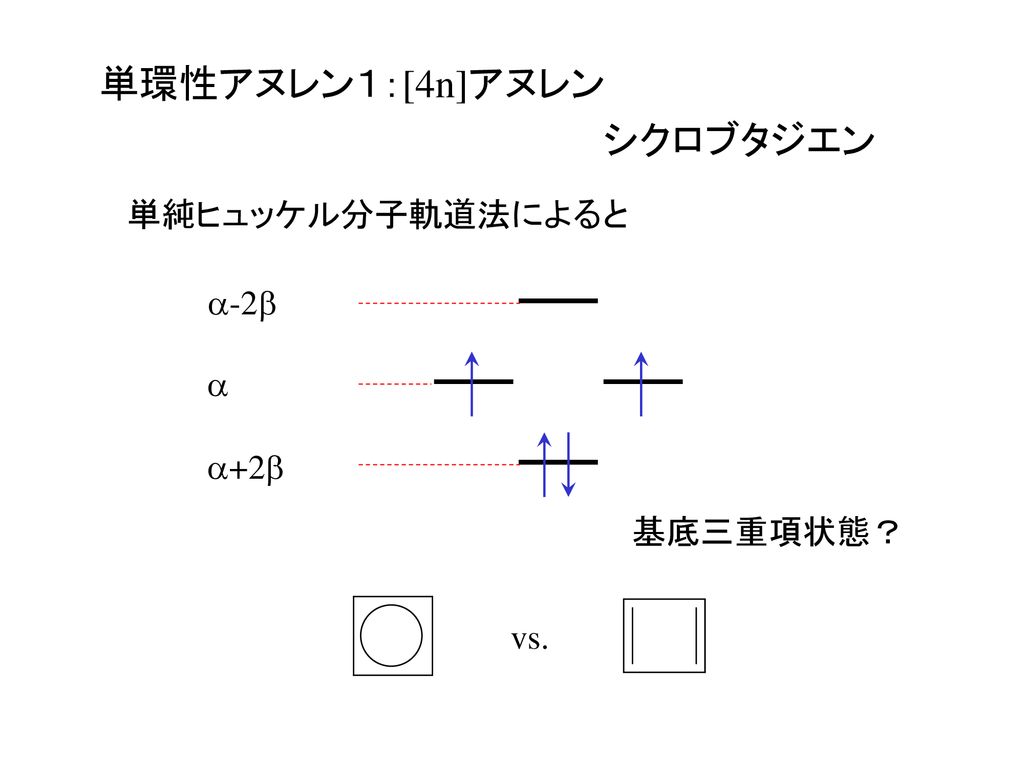



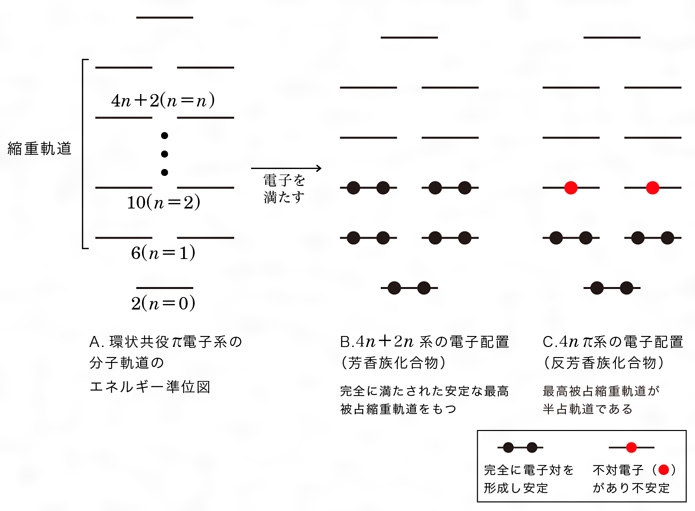
平成18年度 構造有機化学 講義スライド テーマ 芳香族性 奥野 恒久 Ppt Download
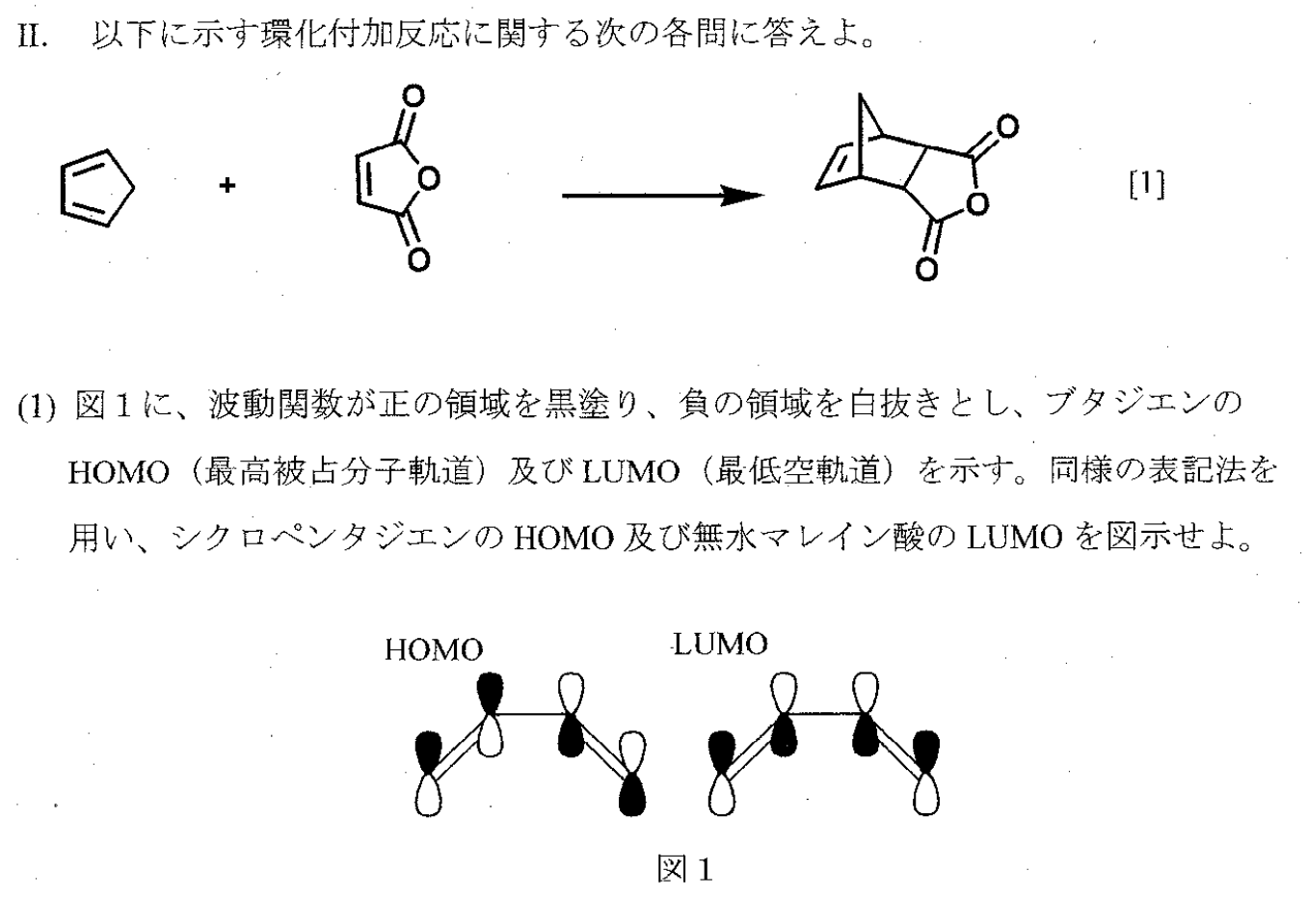



H26 有機化学



Ppt 14 章 非局在化した P 電子系 Powerpoint Presentation Id



Ch3 の分子軌道の構築




ブタジエンはp電子が4つあるのに なぜ1の状態をとるときに横に書くスピンは2 Clearnote



単純ヒュッケル法による分子軌道の計算と共鳴安定化



1 3 5 ヘキサトリエン 分子軌道




第5回



有機反応機構 芳香族求電子置換反応



Misaki Lab Jp




ヒュッケル法 前編 手計算で分子軌道を求めてみた Chem Station ケムステ




ディールス アルダー反応 Wikipedia




雑誌会回答 伊藤



ケトプロフェンの光線過敏症はなぜおこる 薬研




分子軌道法とは サイエンスの人気 最新記事を集めました はてな
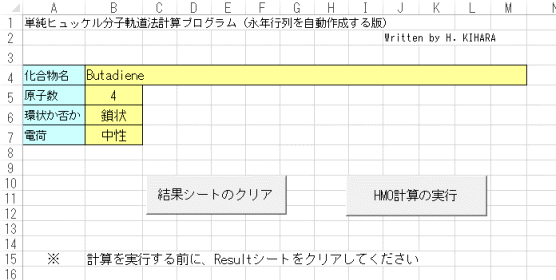



ヒュッケル法プログラムの使い方



ヨウ素とは ヨウ素学会



講義 有機化学1 第15回目の講義から 1 分子軌道法について エチレンとブタジエンのp結合について 片桐教授 東京工科大学 工学部 応用化学科 ブログ



Ttf Pc Uec Ac Jp



Acbio2 Acbio U Fukui Ac Jp
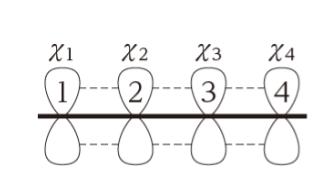



国家公務員総合職 化学 生物 薬学 H29年 問24解説 薬学 これでok



実験8




A A A A C A A A Aœa A



Todai Info
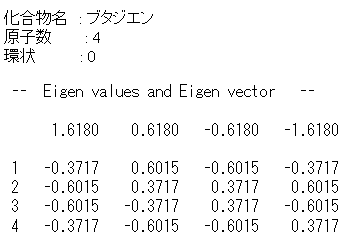



ヒュッケル法プログラムの使い方
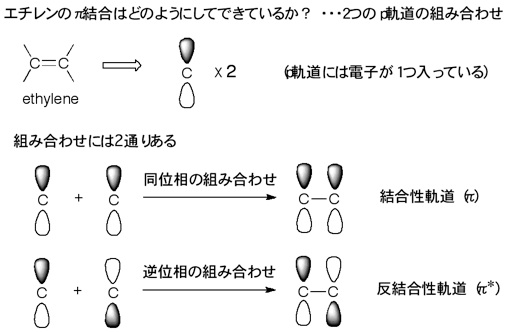



Homoとlumo




日曜化学 3 分子軌道法と可視化 Python Matplotlib Tsujimotterのノートブック
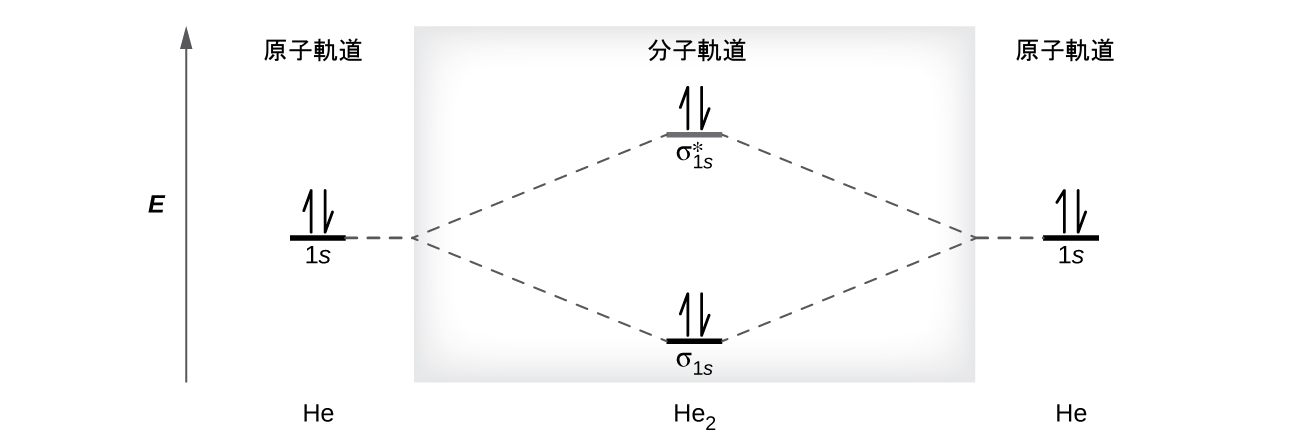



第8章 共有結合の高度な理論 化学 第2版
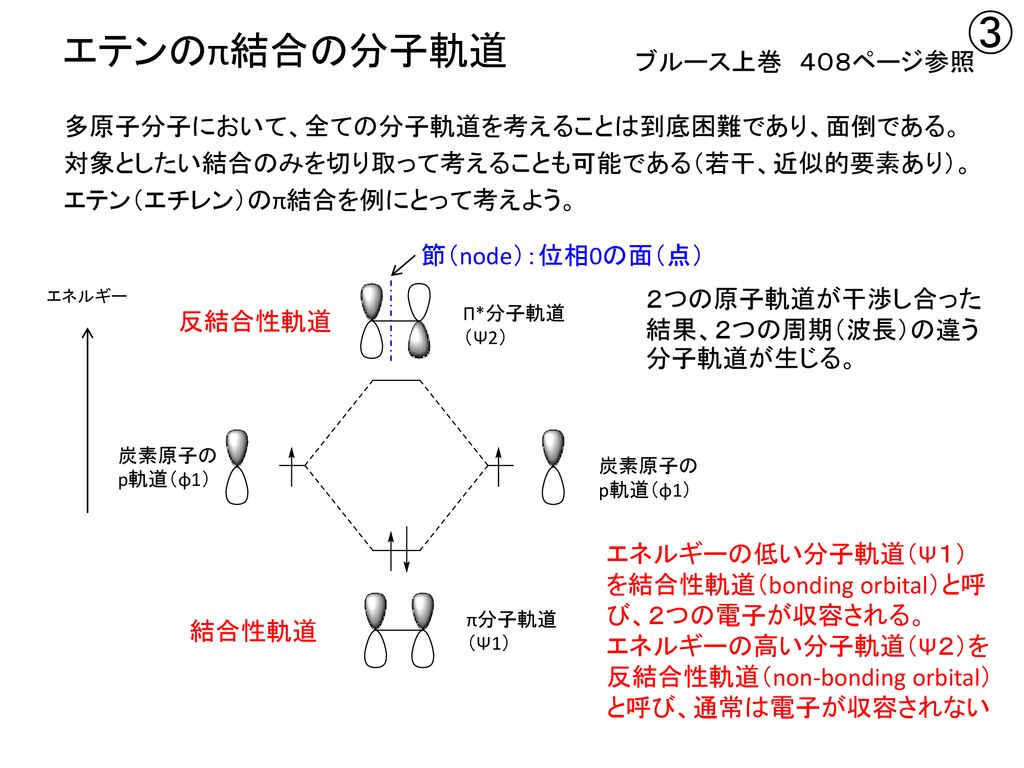



分子軌道理論 Molecular Orbital Theory Mo理論 Ppt Download




ヒュッケル法 前編 手計算で分子軌道を求めてみた Chem Station ケムステ



T Soka Ac Jp



1



Icho Csj Jp
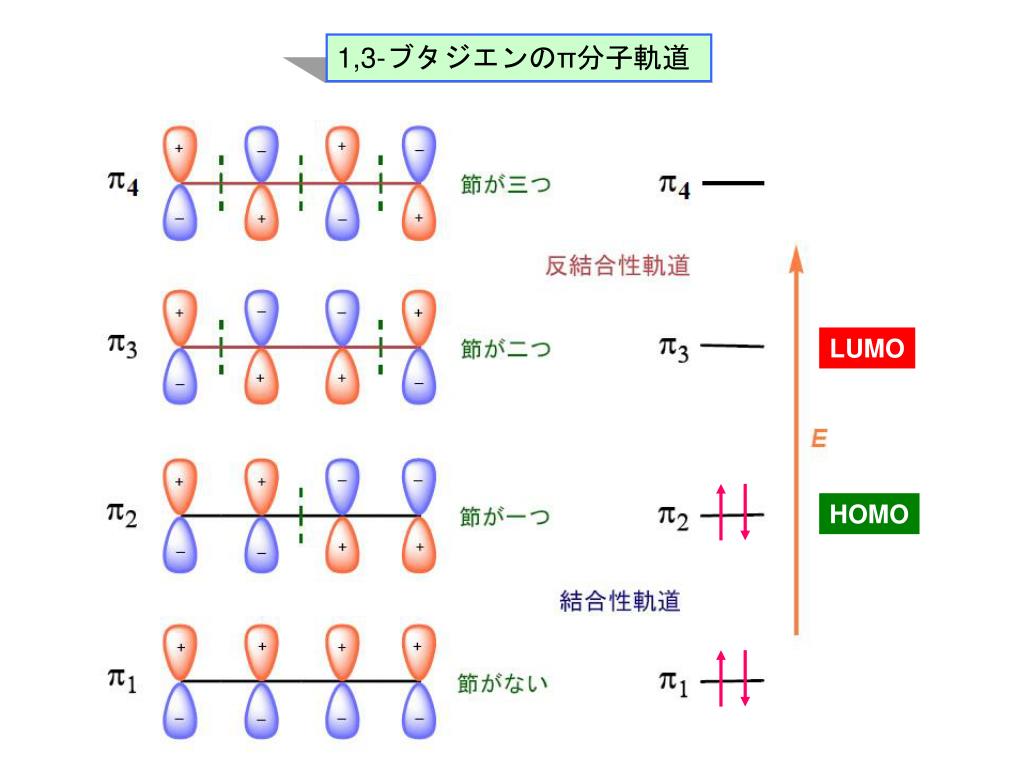



1 3 5 ヘキサトリエン



No comments:
Post a Comment