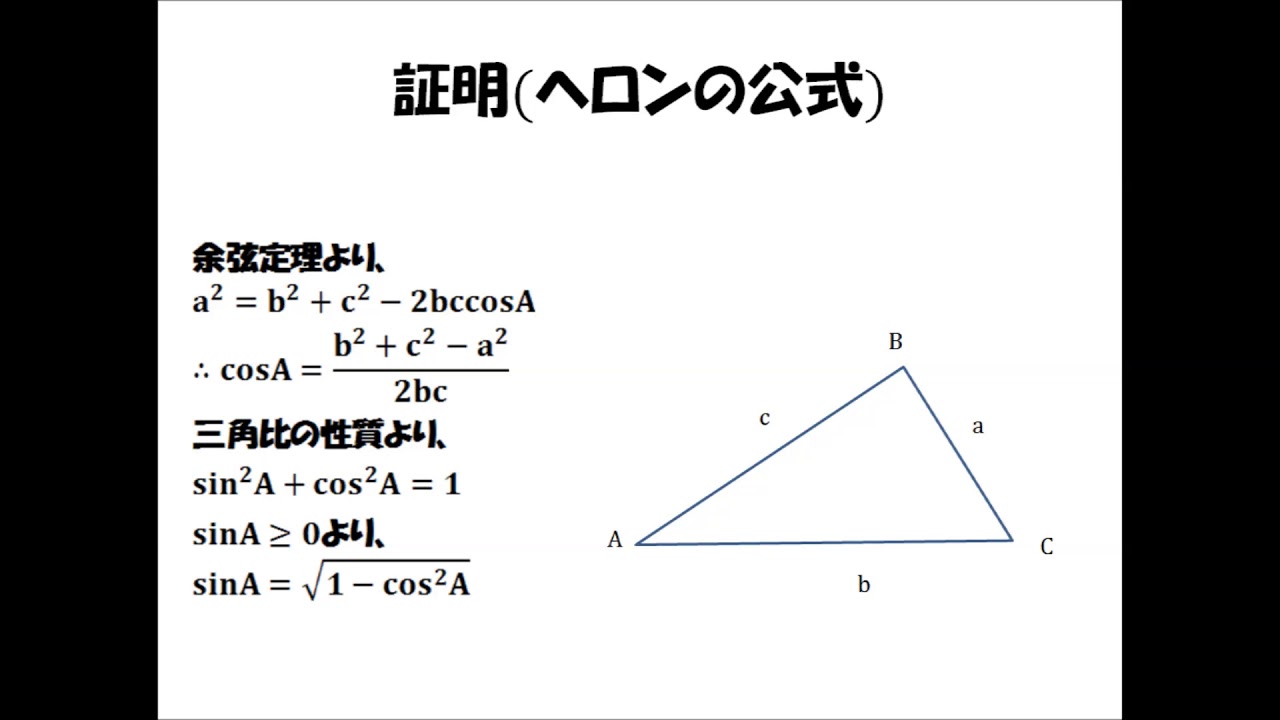
Oct 02, · ヘロンの公式とブラーマグプタの公式について教えてください。ヘロンはいかなる時でも使えるけど四角形だと円に内接していないと使えないんでしょうか? 何故(って言ったら難しい話になりそうだけど)三角形の時はそのまま使えて、四角形は内接が条件なのでしょうか?(間違え三角形の面積を計算する 4つの方法 wikiHow 三角形の3辺が与えられたときの面積の求め方|数学|苦手Feb 03, 21 · 中学数学 数学 高校数学 中学数学で出来る! ヘロンの公式の証明 21年2月3日 ヘロンの公式は、三角形の3辺の長さから面積を求める公式です 以下の三角形ABCの面積Sは S = s ( s − a) ( s − b) ( s − c) ( s = a b c 2) 今回は、この公式の「三角関数を使って証明する方法」と「中学数学だけで証明する方法」の2種類の証明方法を紹介していきます

ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
ヘロンの公式 四角形 証明
ヘロンの公式 四角形 証明-ヘロンの公式の証明 では、なぜこのような公式で面積を求めることができるのか。 三角形のすべての辺の長さがわかっているときに使うと便利• ヘロンの公式は、必ずしも覚える必要はありません。ヘロンの公式とは?公式の証明や、四角形バージョン(ブラーマグプタの公式)もわかりやすく解説! この記事では、ヘロンの公式やその証明について解説していきます。また、四角形バージョンのブラーマ




ブレートシュナイダーの公式 Wikipedia
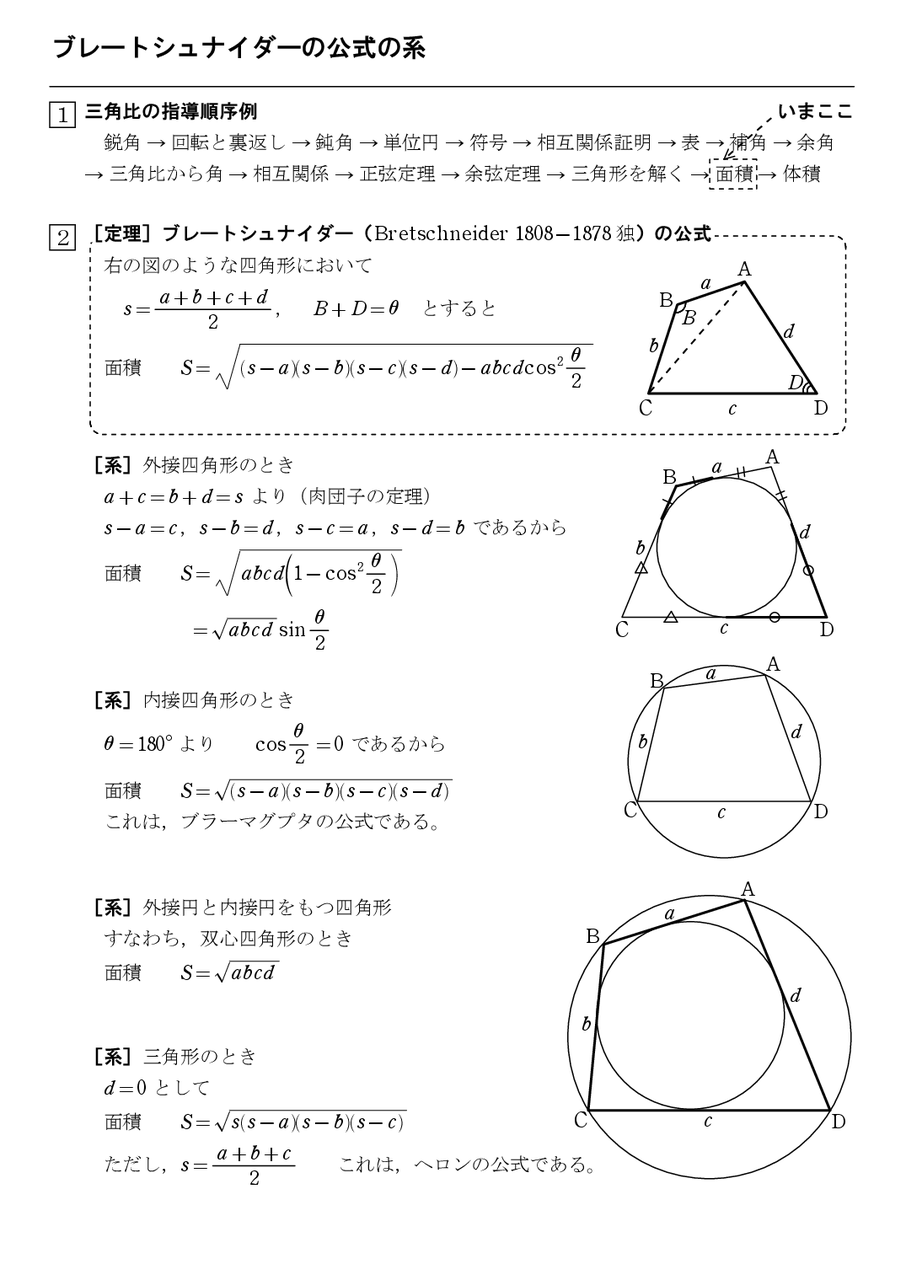
Jun 03, 21 · 陥没地帯 (1) 初等幾何 三角形の面積を求めるヘロンの公式で、三角形の周の長さに関連して s = 1 2(a b c) と置いているが、こう s として置くことはヘロンの公式以外でも便利である。 ABC の内接円が BC = a, CA = b, AB = c と接する点を D, E, F とする。 AE = AF(証明) 四角形の4辺の長さをa,b,c,d,内角をα,β,γ,δとする.ここで,2s=a+b+c+dとおくと,四角形の面積は が成り立つ.この定理でd→0とすると,三角形のヘロンの公式May 02, · 四角形を \(2\) つの三角形に分けて 、三角形の面積の公式「\(\displaystyle S = \frac{1}{2} bc \sin \mathrm{A}\)」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。
Feb 19, 21 · ヘロンの公式とは?証明や、四角形版(ブラーマグプタの公式)も 21年2月19日 内接円とは?内接円の半径の公式や求め方、性質、書き方 練習問題で徹底解説! 21年2月19日 正弦定理とは?公式や証明、計算問題をわかりやすく解説四角形ヘロンの公式, 四角形のヘロンの公式 クリックして Bing でレビューする041 四角形のヘロンの公式 著者 nawadan TV 四角形ヘロンの公式, ヘロンの公式の証明と例題 / 数学I by ふぇるまー ヘロンの公式があれば、次のように計算できます。②Brahmagupta(グラーマグプタ)の公式 4辺の長さが、a ,b ,c ,d である四角形が円に内接し、その面積Sとすると、 証明 Bretschneiderの公式を円に内接する四角形に適用すると、 であるので、 を得る。したがって、 である。
③Heron(ヘロン)の公式 Brahmaguptaの公式において、d=0とすると、 = S s(s−a)(s−b)(s−c)Mar 06, 21 · となりヘロンの公式は使えない(煩雑になる)。 そこで, a 2 = 5, b 2 = 7, c 2 = 9 a^2=5,b^2=7,c^2=9 a2 = 5,b2 = 7,c2 = 9 として上記の公式を用いると, S = 1 4 2 ( 35 63 45) − ( 25 49 81) = 131 4 S=\dfrac {1} {4}\sqrt {2 () ()}=\dfrac {\sqrt {131}} {4} S = 41 2(35 63 45)− (25 49 81)方べきの定理の証明と例題 チェバの定理とその逆 トレミーの定理とは 多角形の内角と外角 中点連結定理 ヘロンの公式 円周角の定理とその逆 直角・鋭角・鈍角三角形の判定法 接弦定理と接弦定理の逆 四角形が円に外接するための必要十分条件




三角比 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月
て学習する「ヘロンの公式」からなるある特殊な場合の三 角形であることを先に述べておく。以下、図8にヘロン 三角形の図形を示しておく。 図8 ヘロン三角形 41 ヘロンの公式 ヘロンの公式は「三角形の3辺 、 、 の長さから面積 𝑆を求める。」 というヘロンの公式の余弦定理による証明と幾何的な証明 図形についての新しい探求 Mathtematics for Teachers ホーム 図形についての新しい探求 中線定理とトレミーの定理による四角形の新しい分類 60°1°になる整数値の辺の三角形 チェバの定理とチェバのデジタル大辞泉 ヘロンの公式の用語解説 三角形の面積Sを3辺の長さa・b・cから求める公式。3辺の和の半分をsとすると、S2=s(s-a)(s-b)(s-c)で与えられる。古代ギリシャの数学者・技術者ヘロン(Heron)によるが、ニュートンが再発見した。




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張
ヘロンの公式やブラーマグプタの公式には長い歴史がありますから,円に内接 する5角形以上の多角形については,辺の長さからその面積を計算する公式がな いことは既に知られていることかも知れないとは思いましたが,一応我々の結果 を英語の論文にしいびつな四角形の面積はどのように計算するのが簡単でしょうか。 そのまえに少し補足です。 kats mizさんが指摘した 『ヘロンの公式』 とは次のような式の事です。 補足図1 三角形の3辺の長さだけで三角形の面積が求まる便利な公式であり、 紀元前300年よりもさらに昔から知られていたブラマグプタの公式 インドの数学者ブラマグプタ(598~660)は、とても美しい公式を残している。 そして、この公 式のおかげで、長年多少違和感のあった「ヘロンの公式」が、実は必然的なものであることが 理解できた。 ブラマグプタに大いに感謝しなければならない。 ブラマグプタの公式 円に内接する四角形の4辺の長さを、a、b、c、d とするとき、 四角




この問題なんで Ahbや Abhに着目して考えるのか分かりません 解説お願いし Clear




書籍紹介詳細ページ
ヘロンの公式(ヘロンのこうしき、英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 アレクサンドリアのヘロン が彼の著書『 Metrica 』の中で証明を与えていることから彼に帰せられる 1 。ヘロンの公式 の用例・例文集 円の内接四角形の面積を求めるその式は、ヘロンの公式を内包している。ヘロンの公式はこれらの公式の特別な場合となっている。これは三角形におけるヘロンの公式を一般化したものである。これは三角形の面積を辺の長さで表すヘロンの公式と面積公式をヘロンの公式において, この隠された関係が公式が正しいことを示す上で最もエレガントな方法です。 回答の1番下にヘロンオリジナルの幾何を使ってこの関係を証明しますが, まずは色のついたそれぞれの三角形のペアを並び替えることで x y z の和がこの三角形の面積に等しいことを示させ




最新三角形 の 公式 小学校 最高のぬりえ
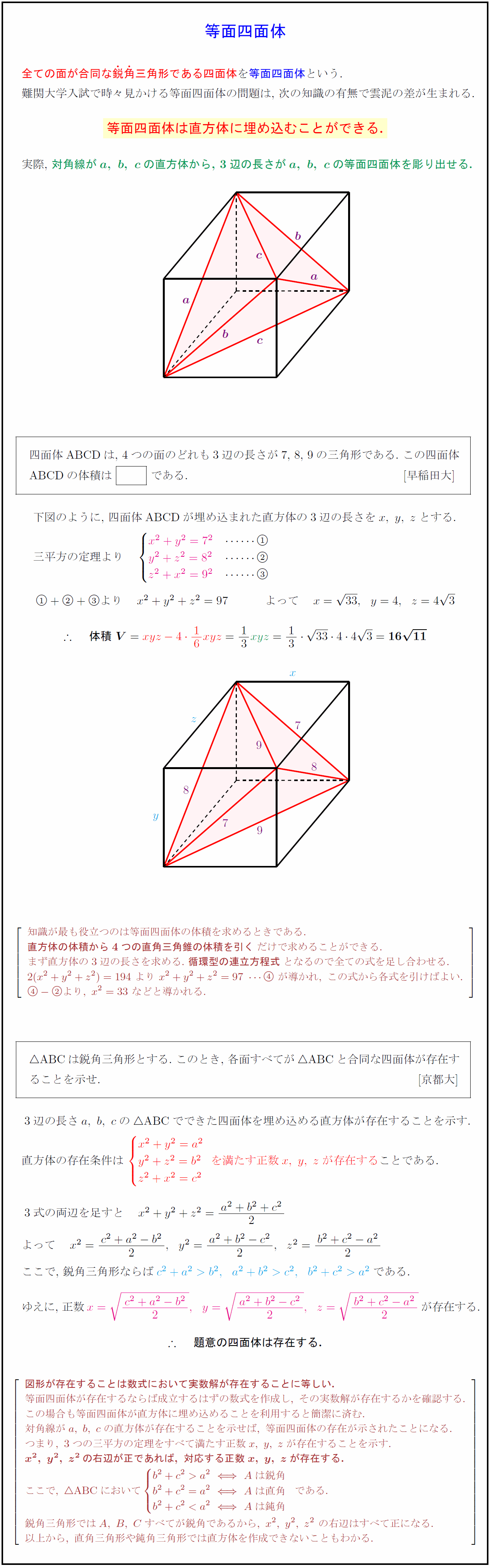



高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月
四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 5152 一対の対角(の和)が判っていれば,ブレートシュナイダーの公式(Bretschneider's formula) が使えますが,ここでは「長さ情報」のみを使用しています. 辺ABの長さこの公式はアレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられるが、現代ではこれ自体は シラクサ の アルキメデス にも既知であったと考えられていて、さらにそれ以前から知られていた可能性もある。Page 5 この公式において,辺の長さd を限りなく0に近づけると四角形は三角形となりヘロンの公式を得る. 四角形の面積公式から眺めると,s は「周の長さの半分」と捉える方が自然といえるのである. ブラマグプタ(598~660)は,アリヤバータ(476~550)とともにグブタ王朝時代のインドを代表す




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典
ヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a, b, c の長さから 面積S を求める公式である。三辺から三角形の面積計算(ヘロンの公式) 法面展開図、舗装面積、出来形展開図を作成するには必要な計算です。 現場で3辺を測定しながら、その場で面積計算できるアプリです。 ヘロンの公式だけでなく、実際に現場で利用できる面積計算の登録ができます。 建設現場で実際に使い三角形の求積方法にヘロンの公式(6) が存在するように, 各辺の長さと対角の大きさから四角形の面積S を 求めるブレートシュナイダーの公式(7) が知られている S = √ (T p)(T q)(T r)(T s) pqrscos2 \A\C 2 ただし, T = pqr s 2 (7) ブレートシュナイダーの公式は次の
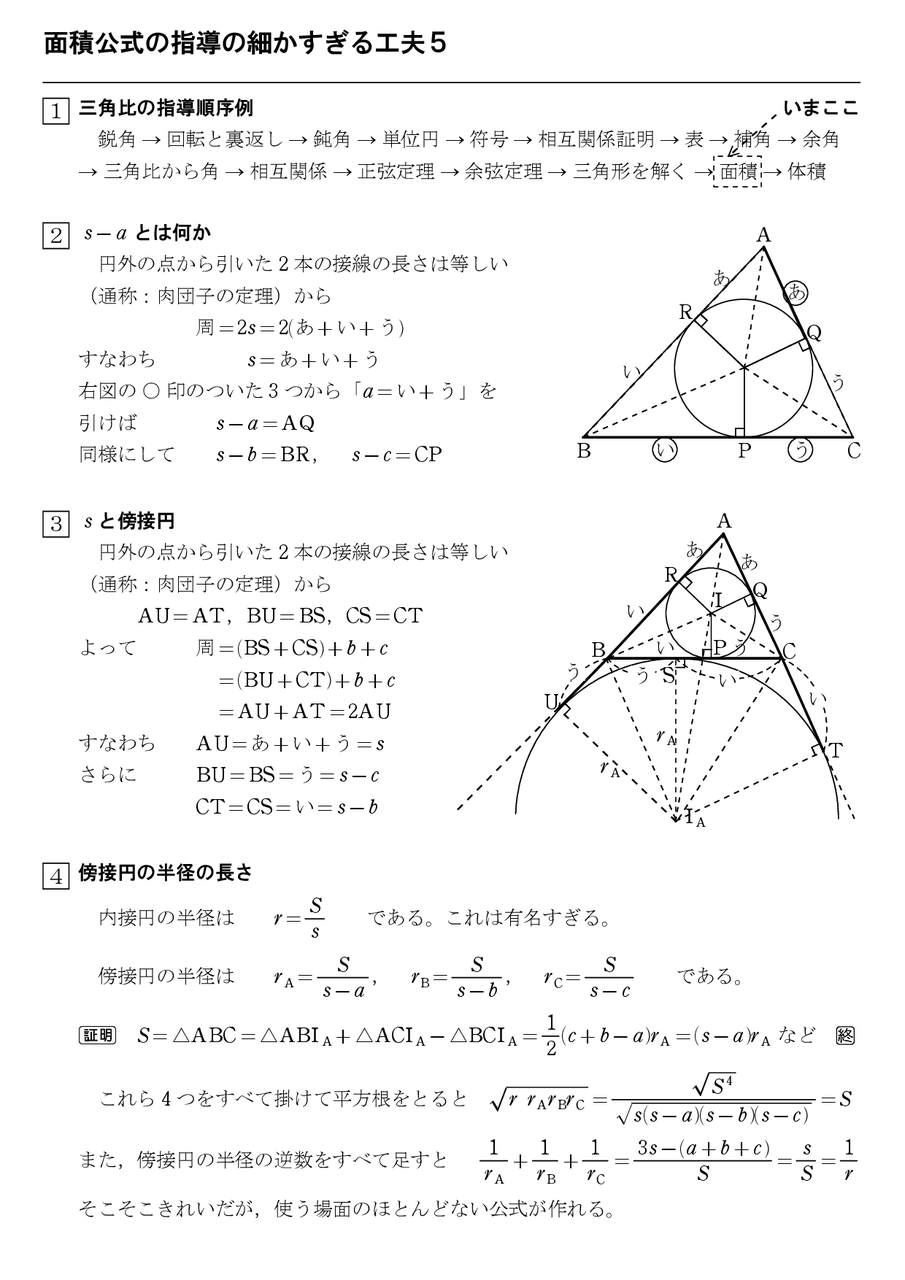



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典
小学算数の面積の求め方と公式一覧!四角形・長方形の性質や ヘロンの公式の証明と使用例 高校数学の美しい物語;ヘロンの公式とは、三角形の3辺の長さから面積を求める公式のことである。 長さ a,b,c の線分を辺とする三角形(左画像)があり、s=(abc)/2 と置く。 この場合の三角形の面積を S とした場合に下記の公式が成立する。ヘロンの公式(ヘロンのこうしき、英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる 。 目次 1 概要




色んな図形の面積の求め方 小学4年の算数の問題です 教科書で確認した Okwave




ヘロン の 公式 証明



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典
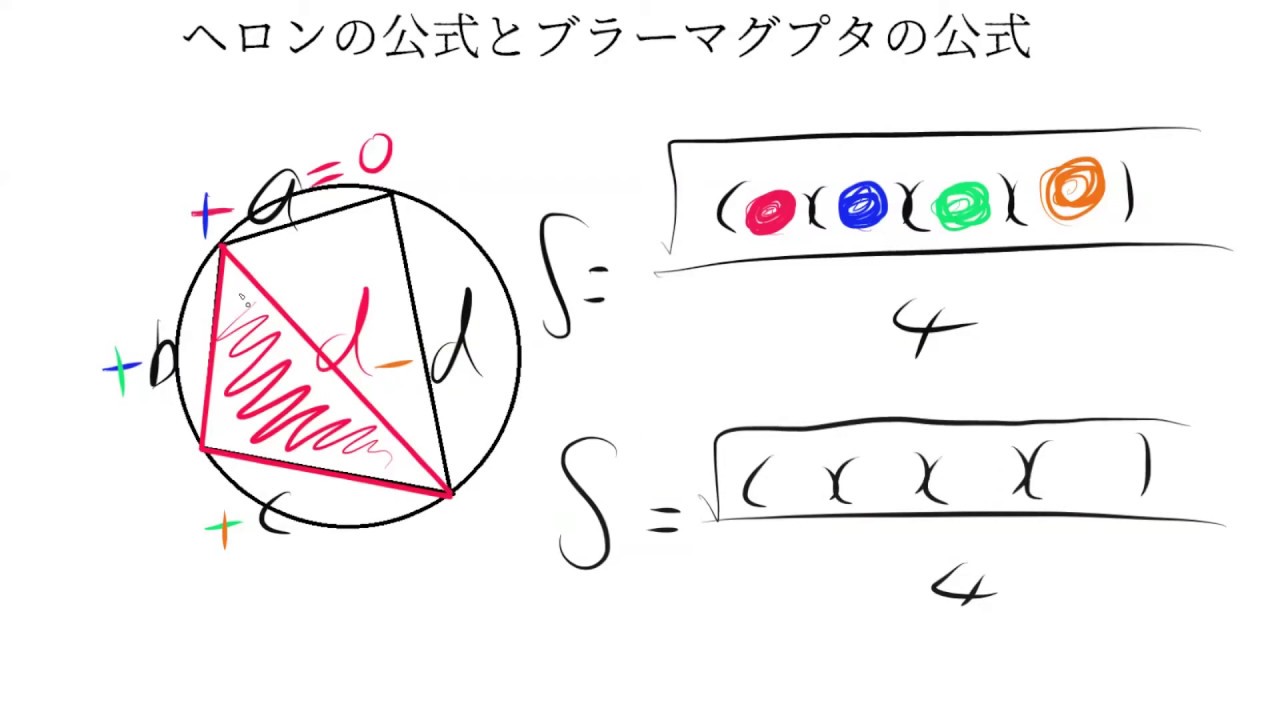



ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube




内接円と外接円の一致の証明 お世話になります 平面幾何に関する証明問題 Okwave




高校数学 トレミーの定理 裏技 の三角比による証明と幾何的証明 記述試験で無断使用できる 受験の月




79 ヘロンの公式 三角形と内接四角形 両方解説 ブラーマグプタの公式 Youtube




ブレートシュナイダーの公式 Wikipedia
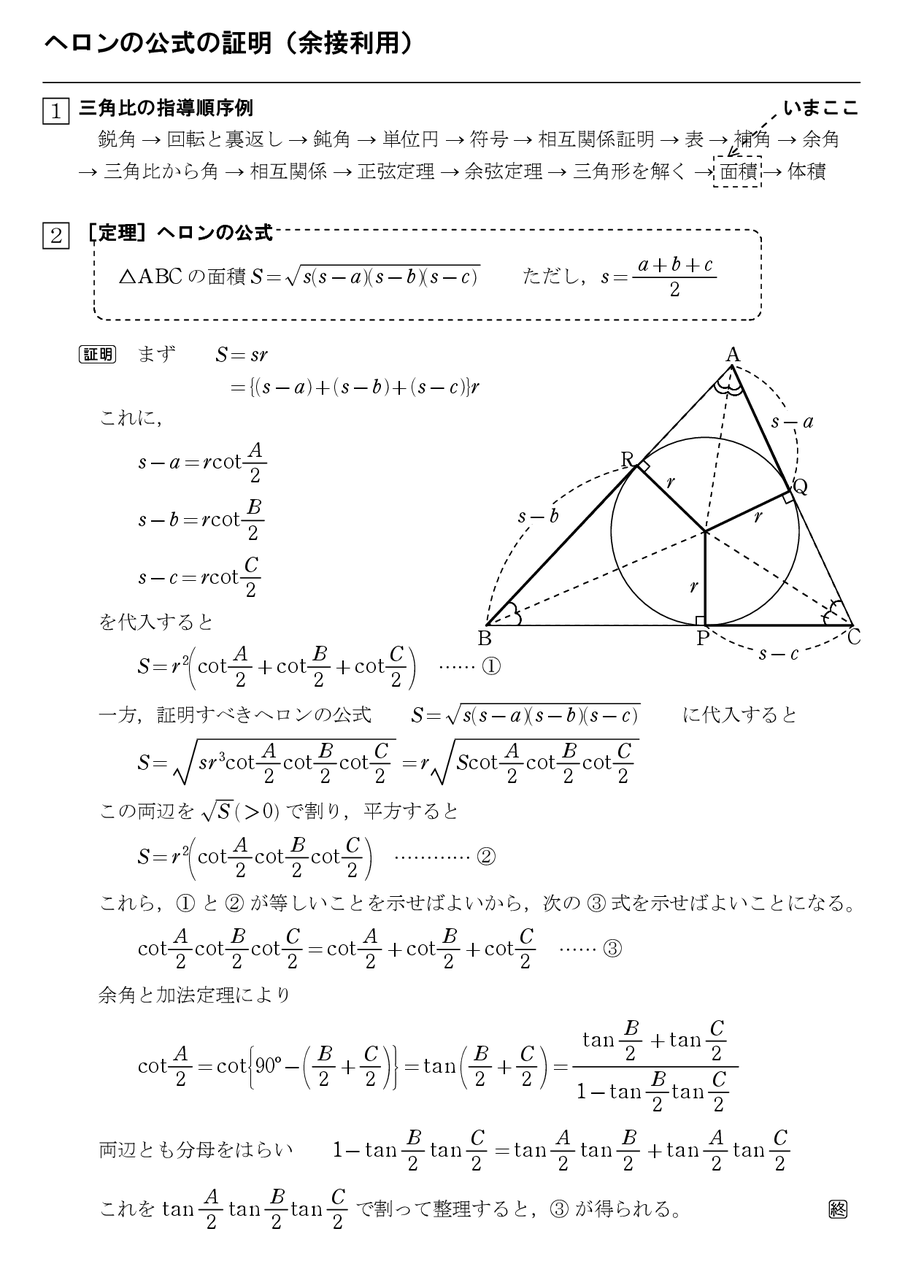



15年08月 怜悧玲瓏 高校数学を天空から俯瞰する




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する
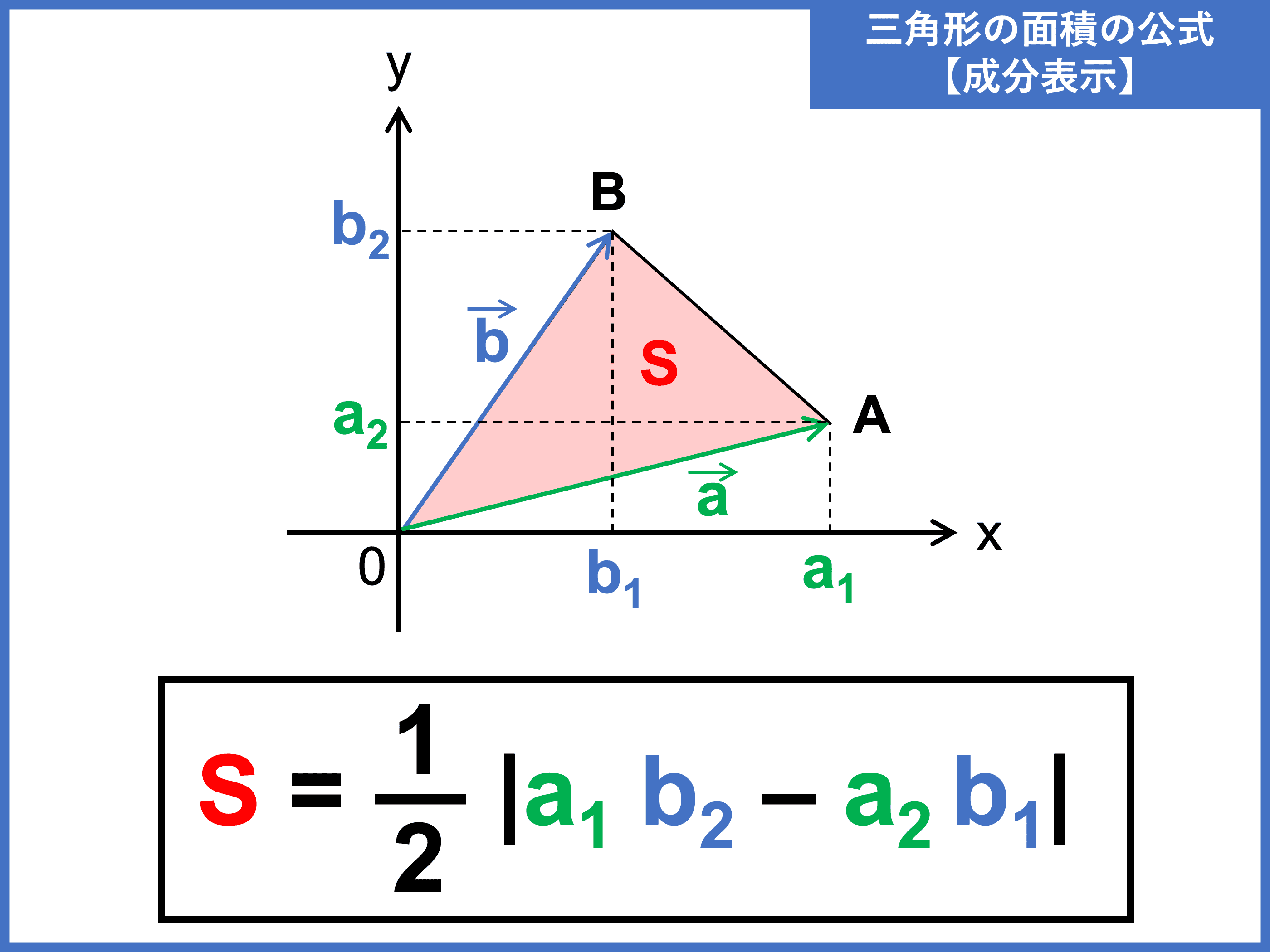



三角関数 面積 公式 証明
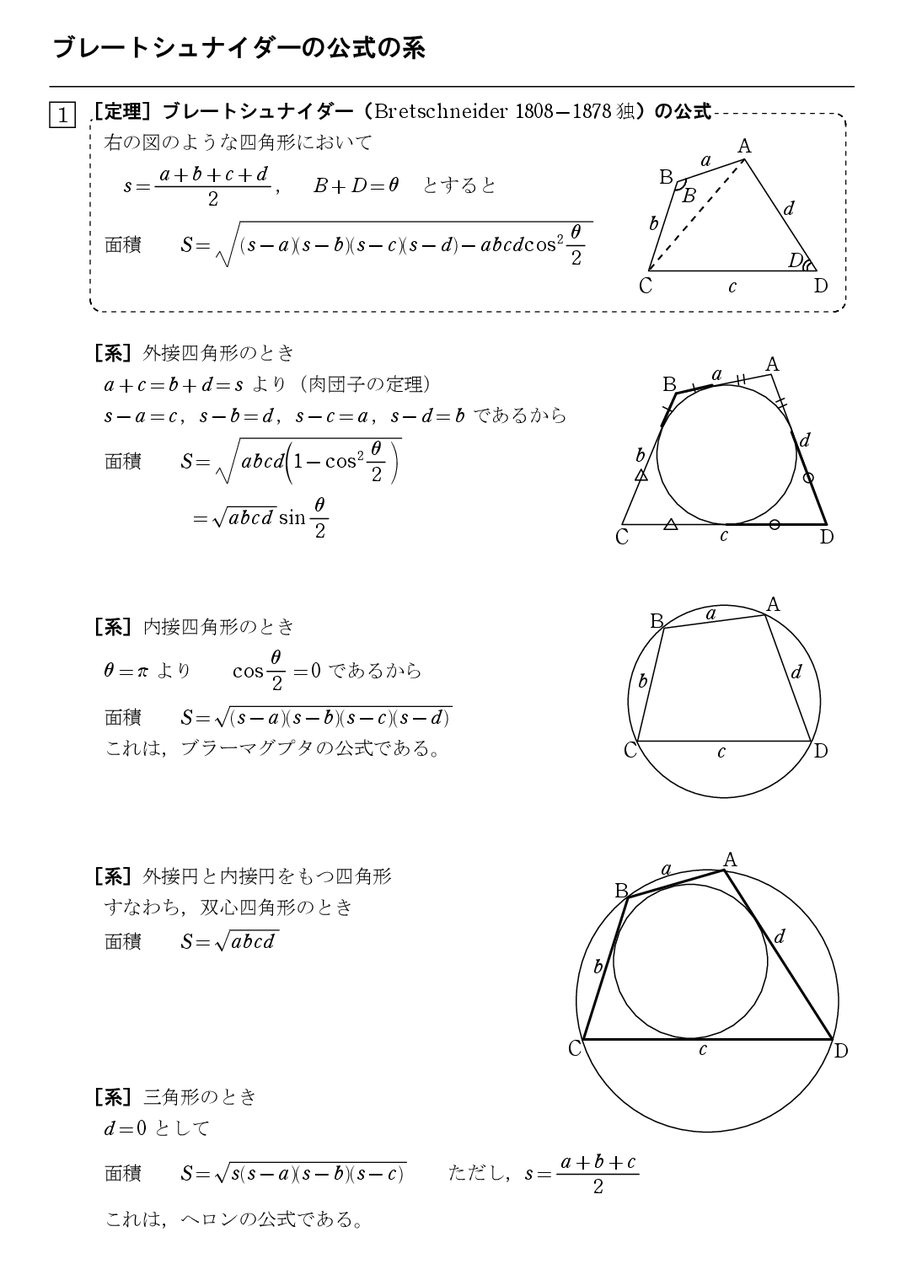



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート
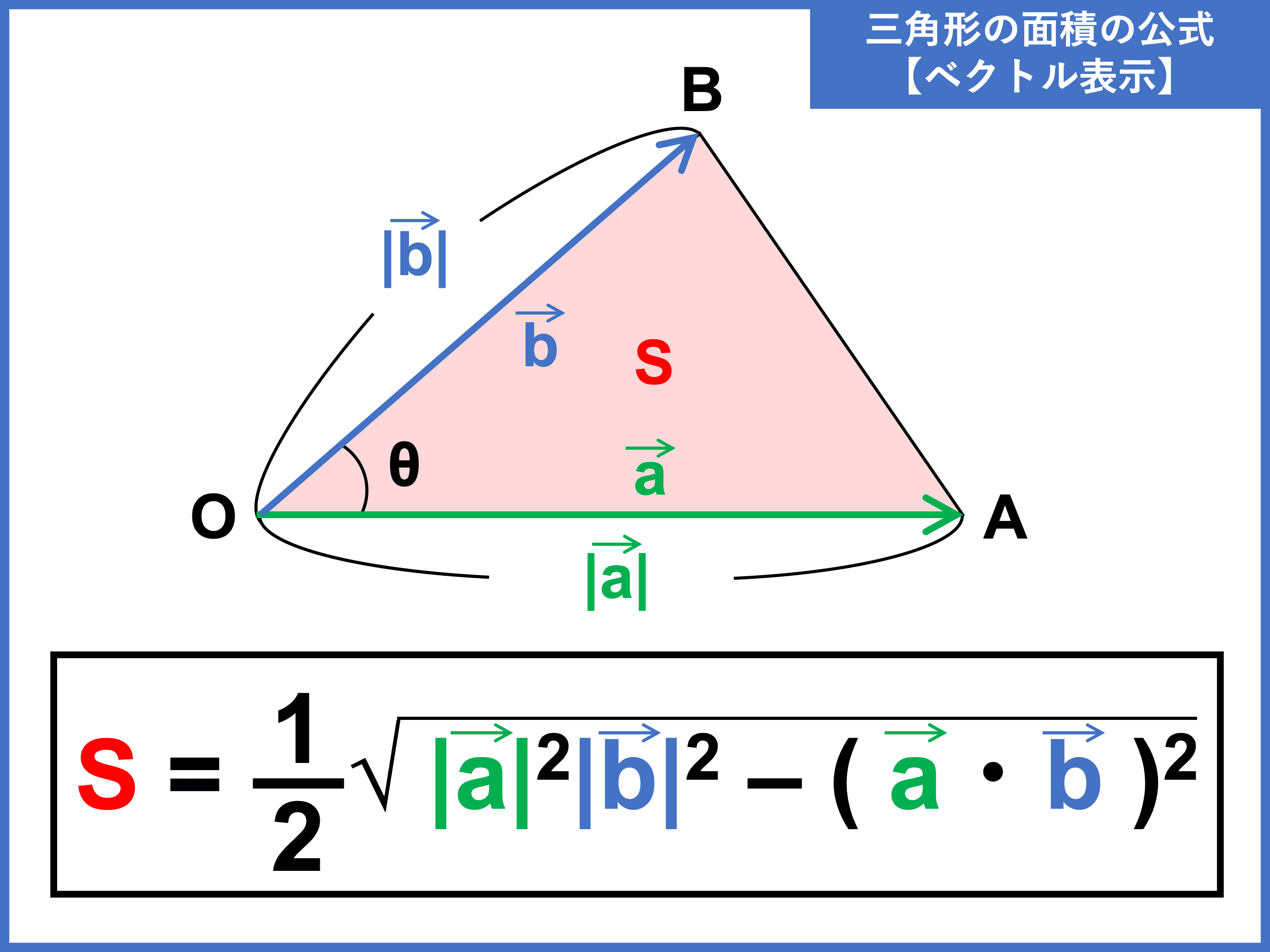



三角関数 面積 公式 証明




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




正方形の中にある三角形の面積の平均 Musyokutoumei
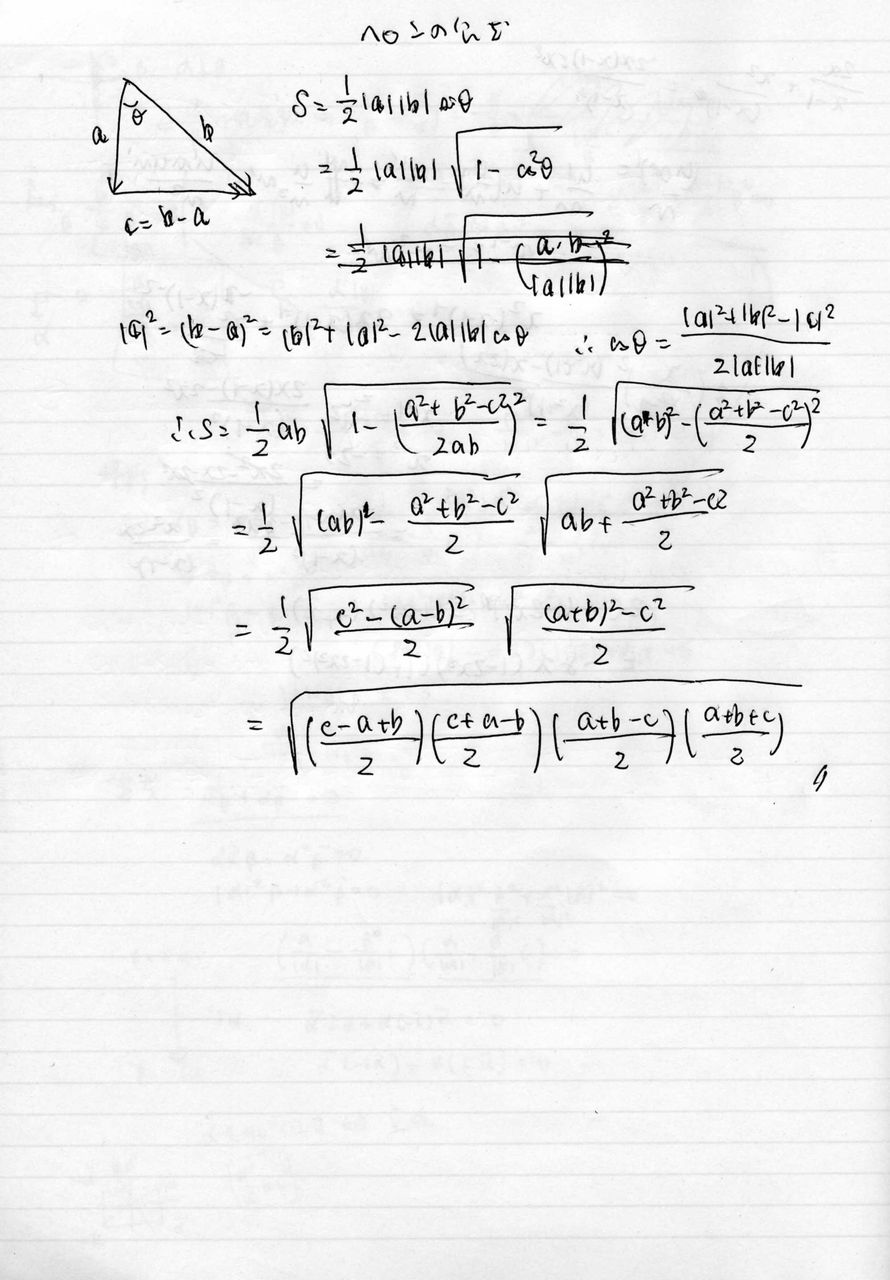



17年08月24日 東大合格コム




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
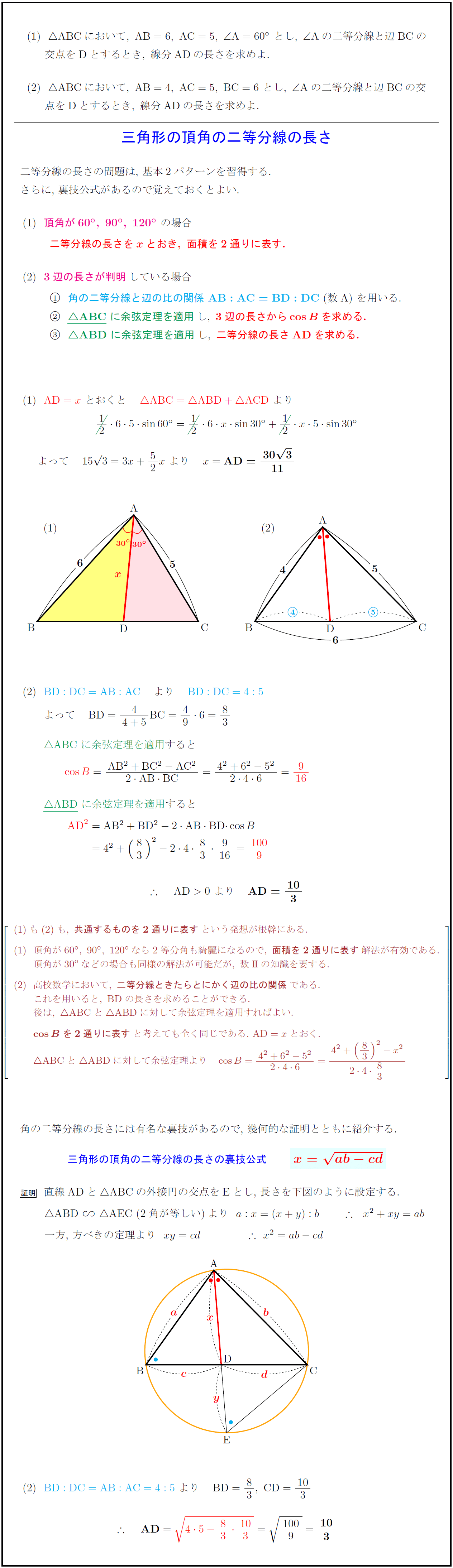



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




高校数学 円に内接する四角形の対角線の長さと面積 受験の月




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
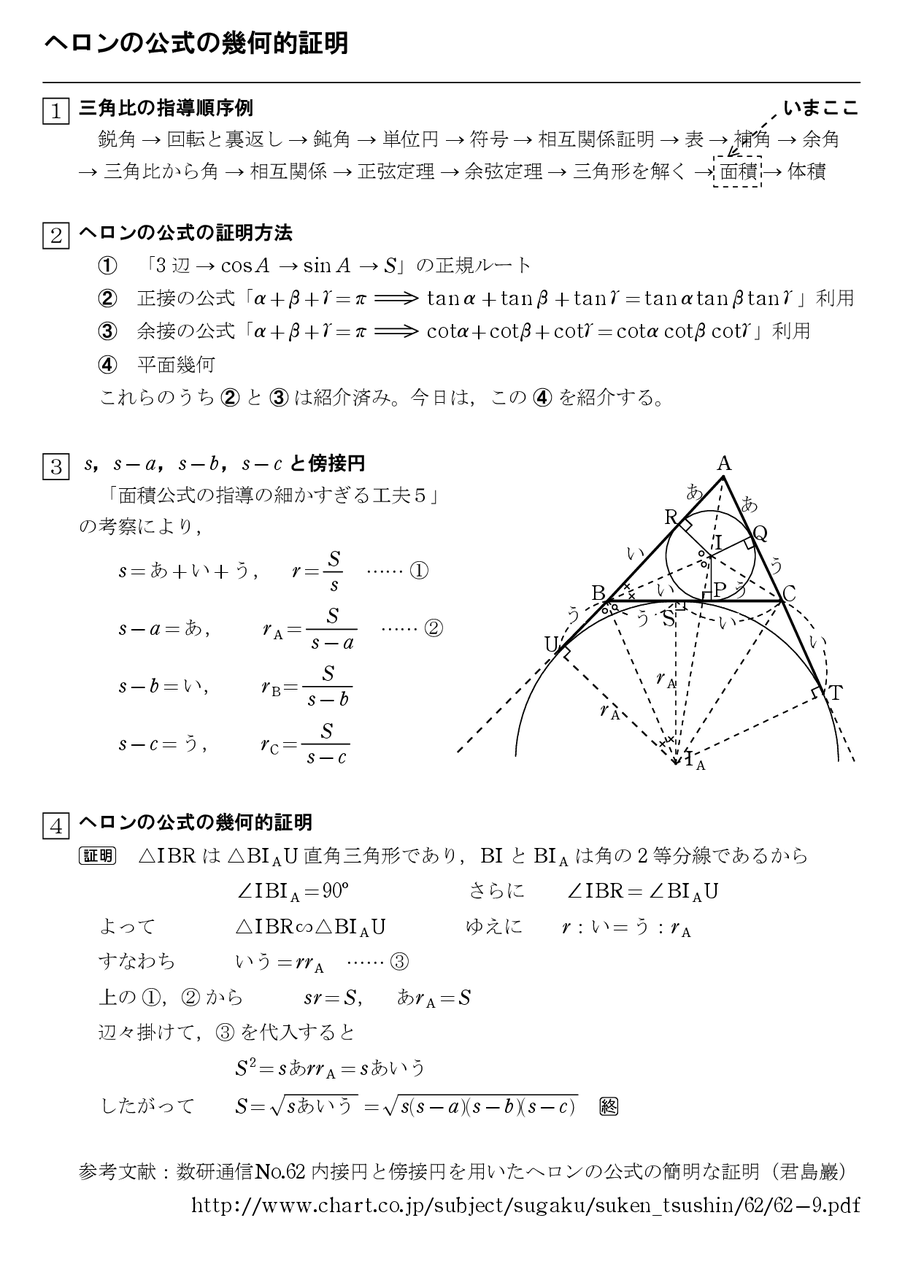



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




17年08月24日 東大合格コム



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




新鮮な四角形 対角線 長さ 求め方 最高のぬりえ




ブラーマグプタの公式 東大合格コム




3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート




無料ダウンロード底辺高さ2 証明 最高のぬりえ
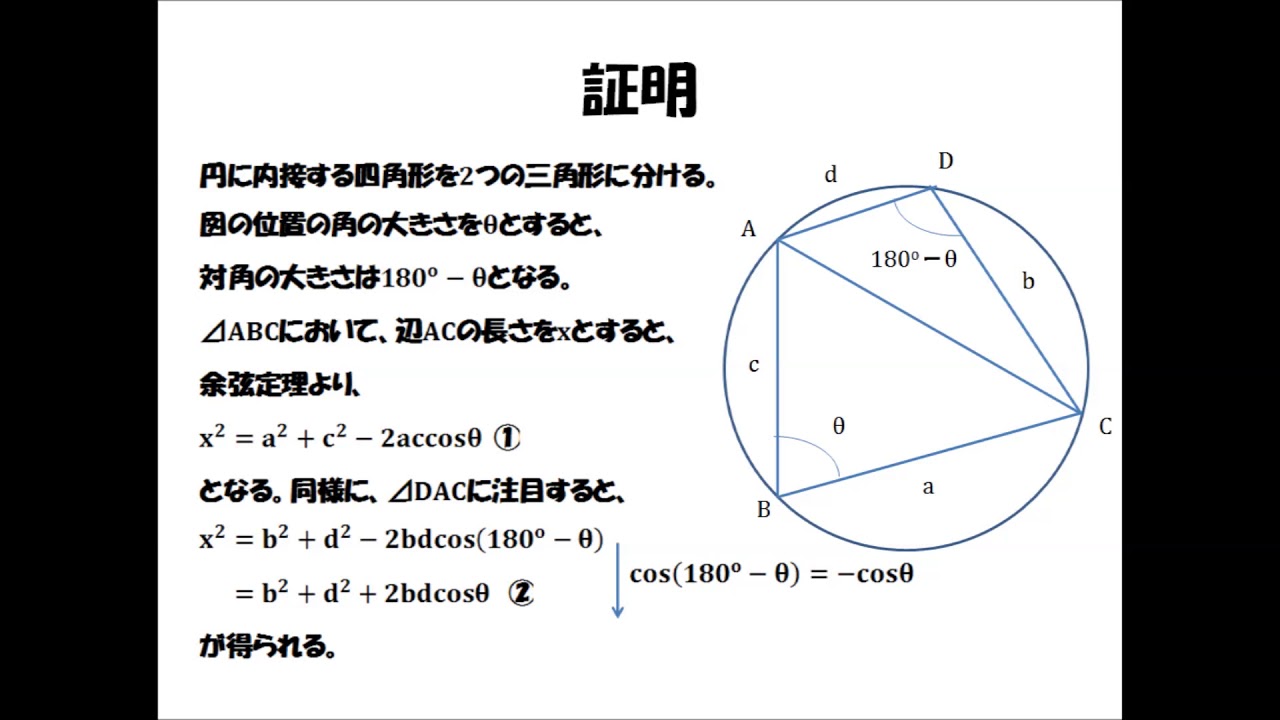



Haruka先生の数学証明シリーズ ブラーマグプタの定理 Youtube
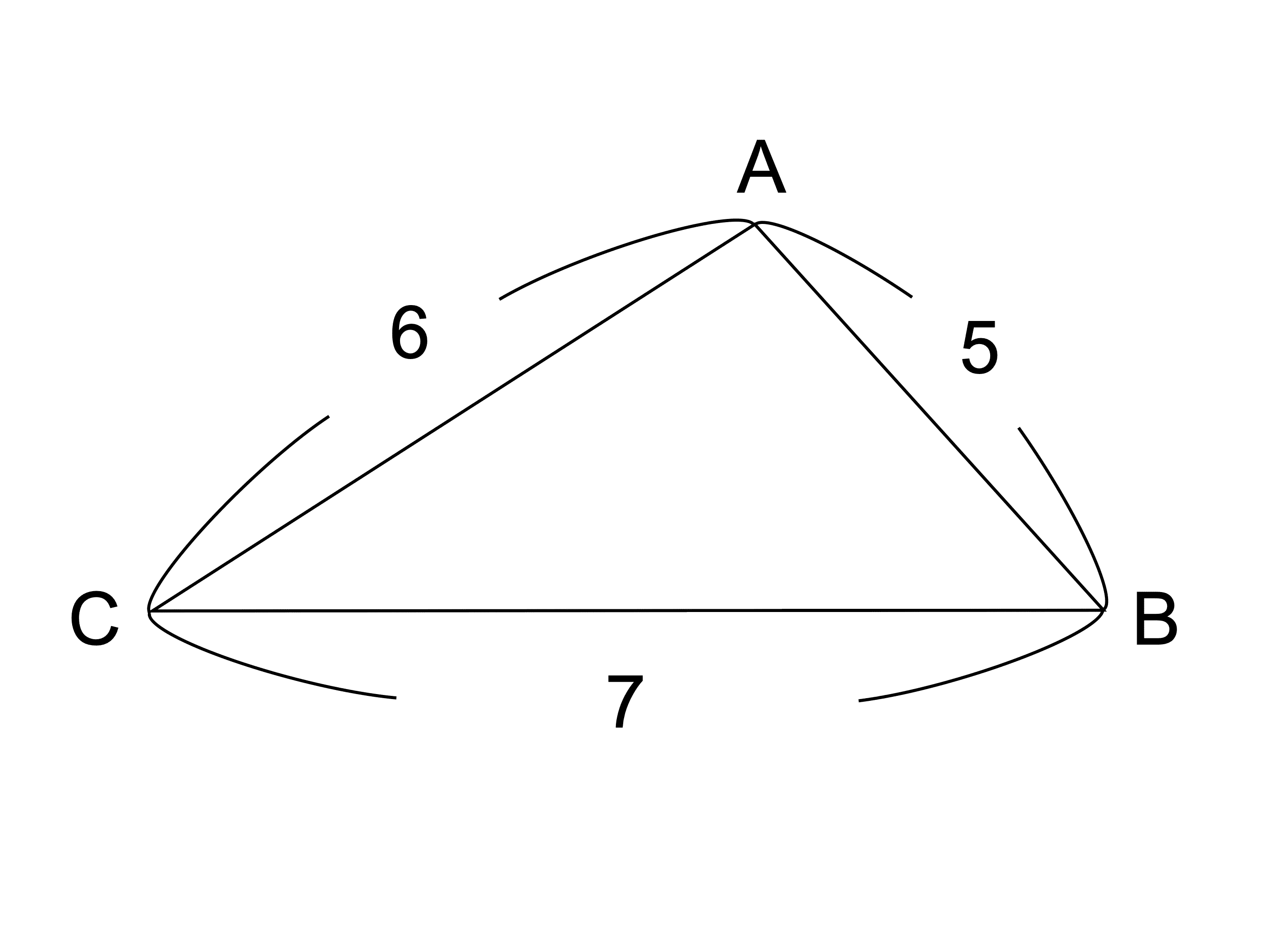



Images Of ブラーマグプタの公式 Japaneseclass Jp




三角比 怜悧玲瓏 高校数学を天空から俯瞰する



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



Wmhzeavgi2oi8m




三角比の添削 追記9月14日 Matsu Math Note




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



ヘロン の 公式 証明



トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ




ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月



トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ




高校数学 数 94 三角形の面積 ヘロンの公式編 Youtube




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
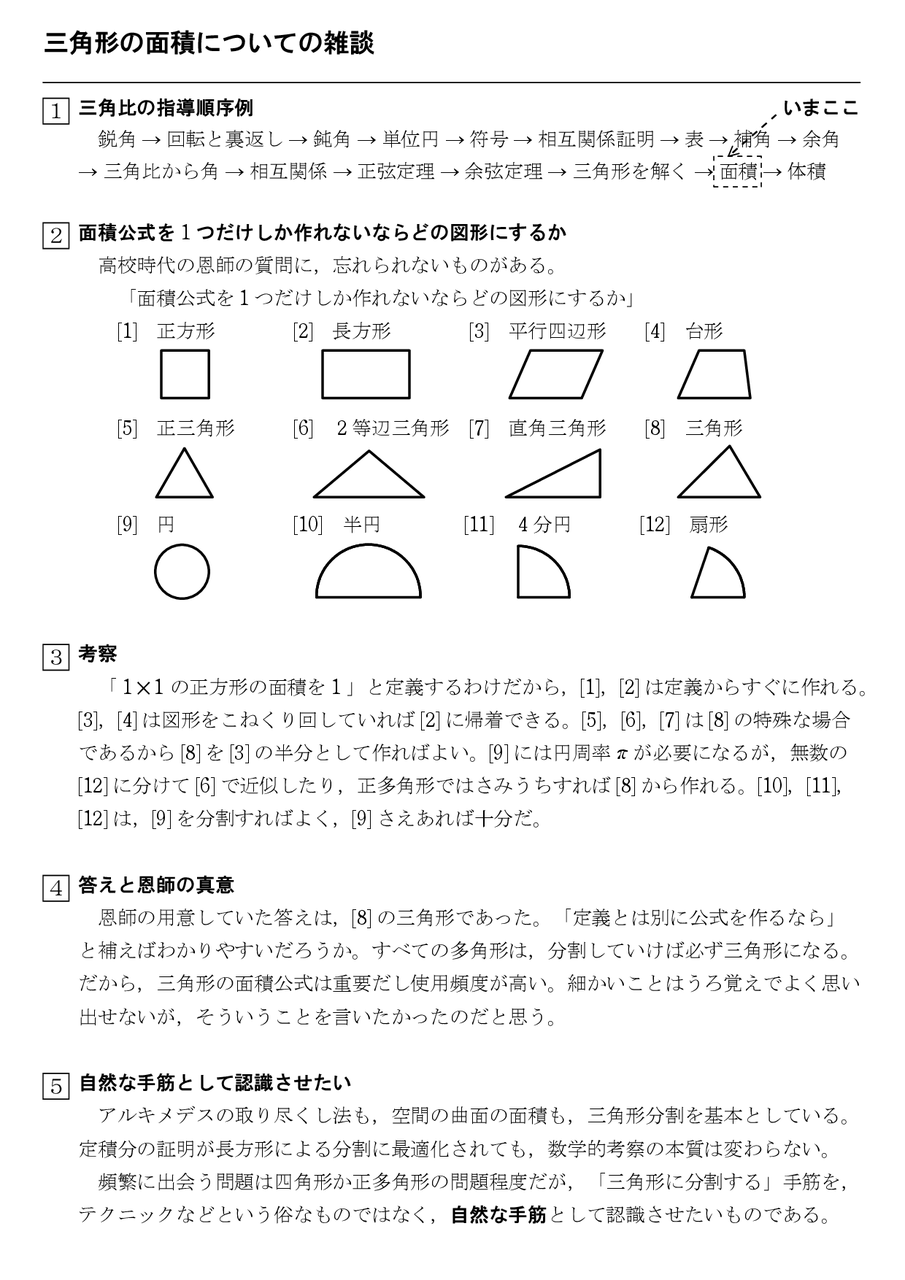



15年08月 怜悧玲瓏 高校数学を天空から俯瞰する
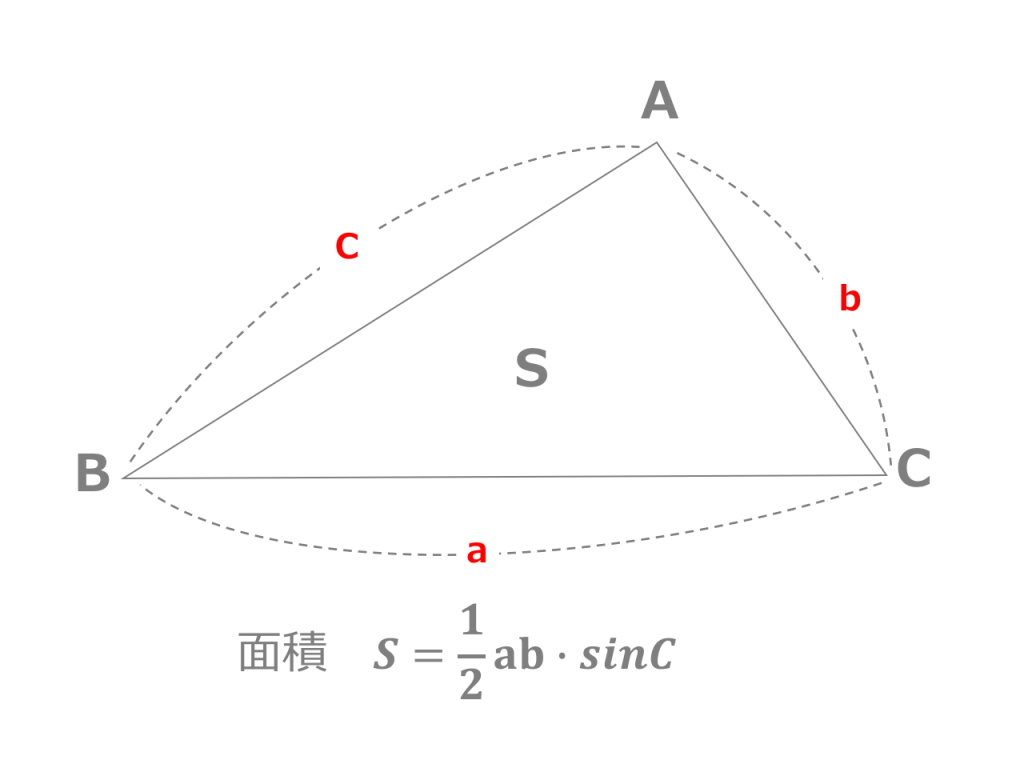



三角関数 面積 公式 証明
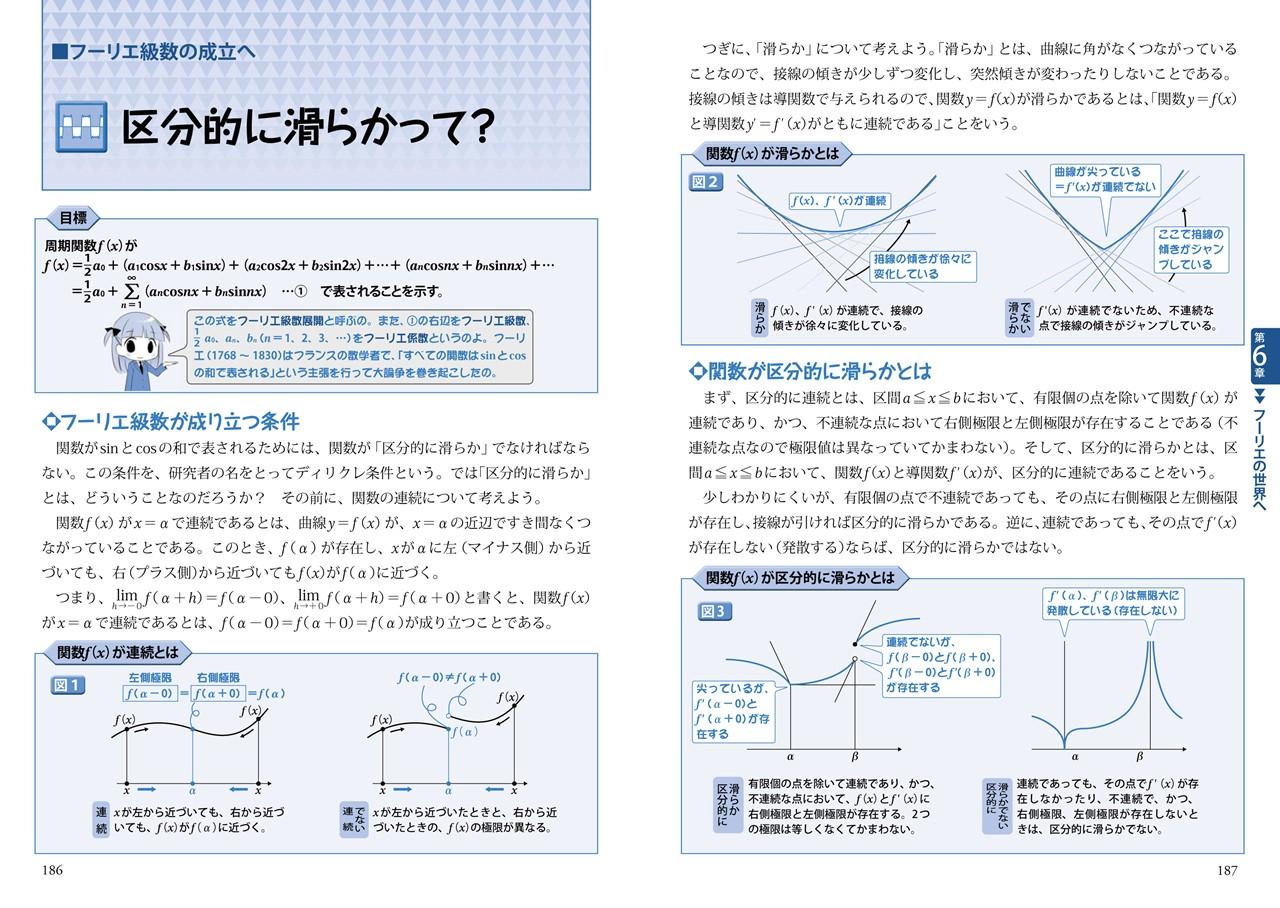



史上最強図解 これならわかる 三角関数 ナツメ社
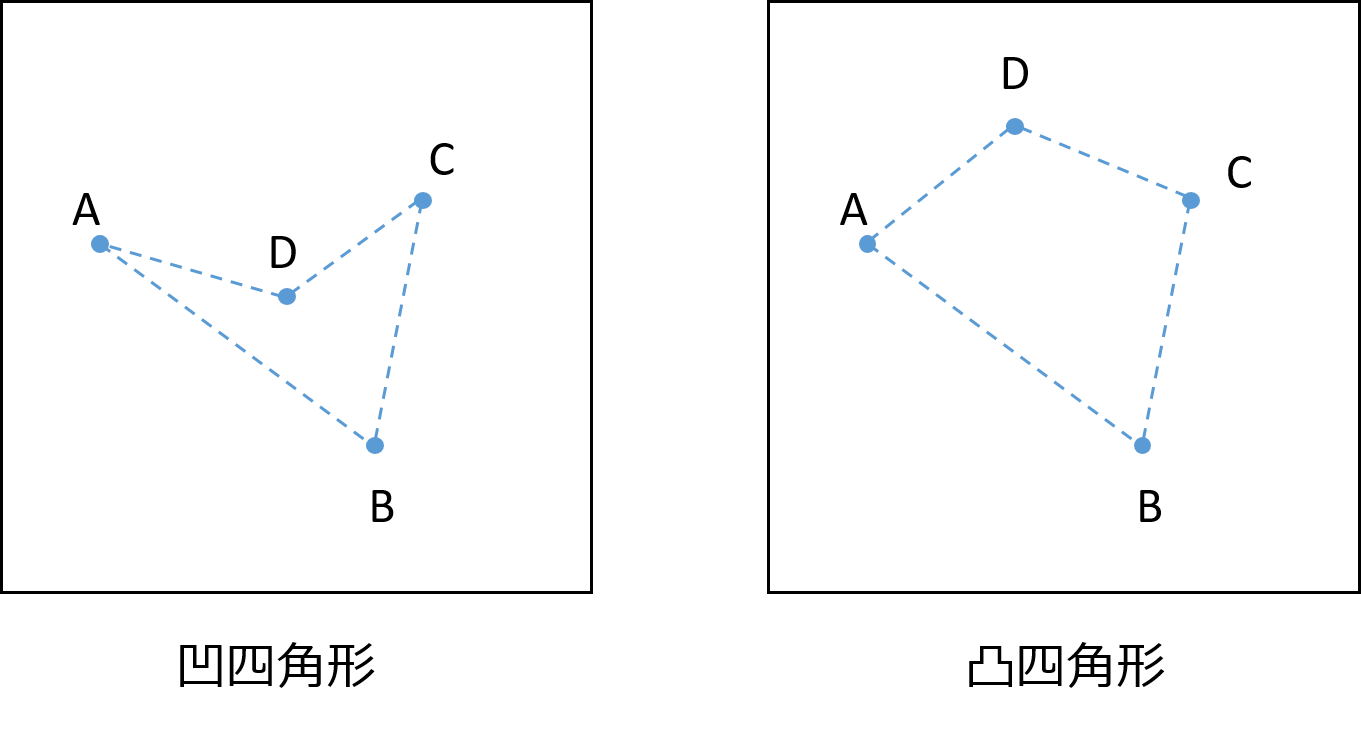



正方形の中にある三角形の面積の平均 Musyokutoumei
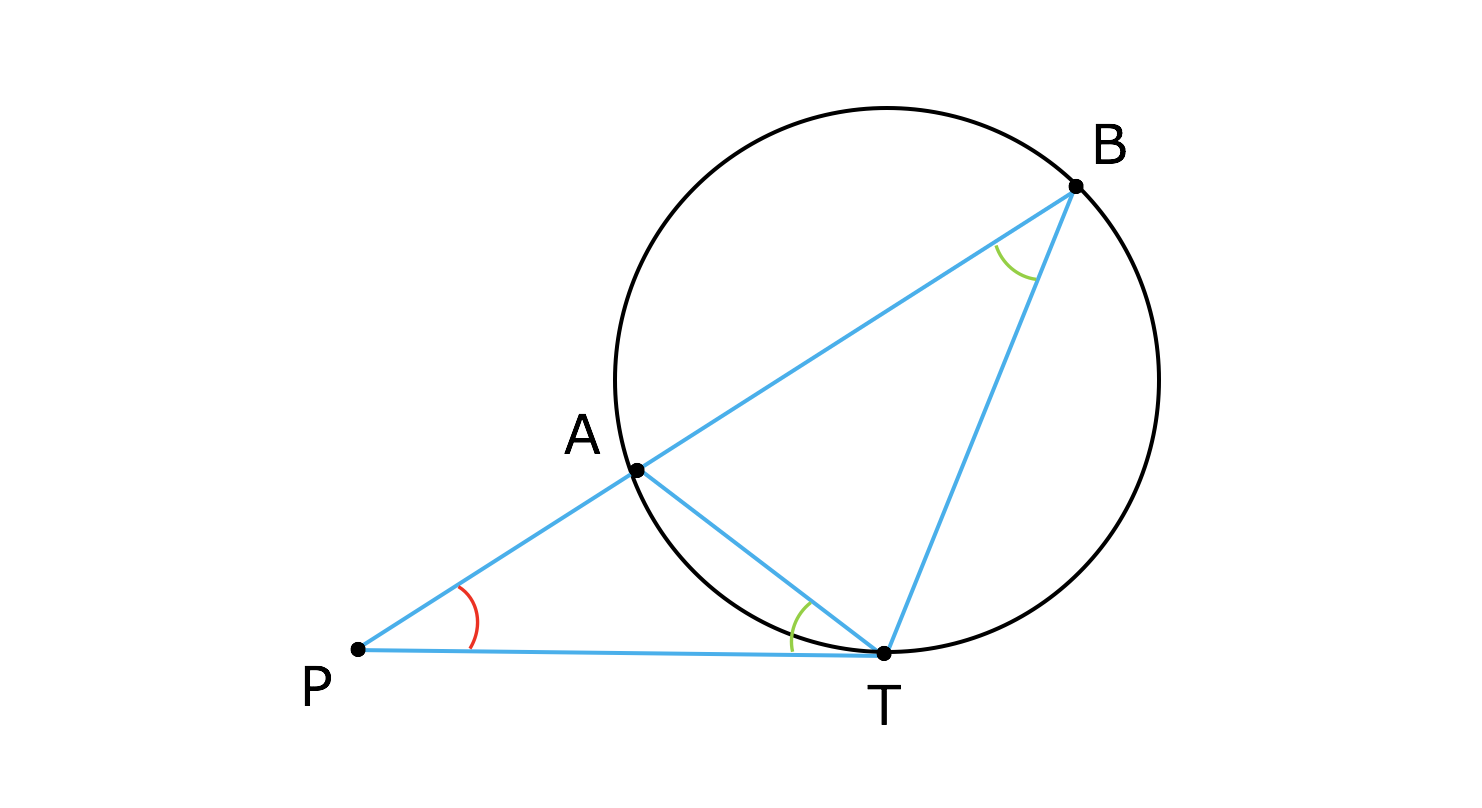



3分で分かる 方べきの定理の証明 使い方 合格サプリ




3分で分かる 方べきの定理の証明 使い方 合格サプリ




三角比の面積 公式と計算方法は いろんな場面での使い方を解説 数スタ




史上最強図解 これならわかる 三角関数 ナツメ社




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
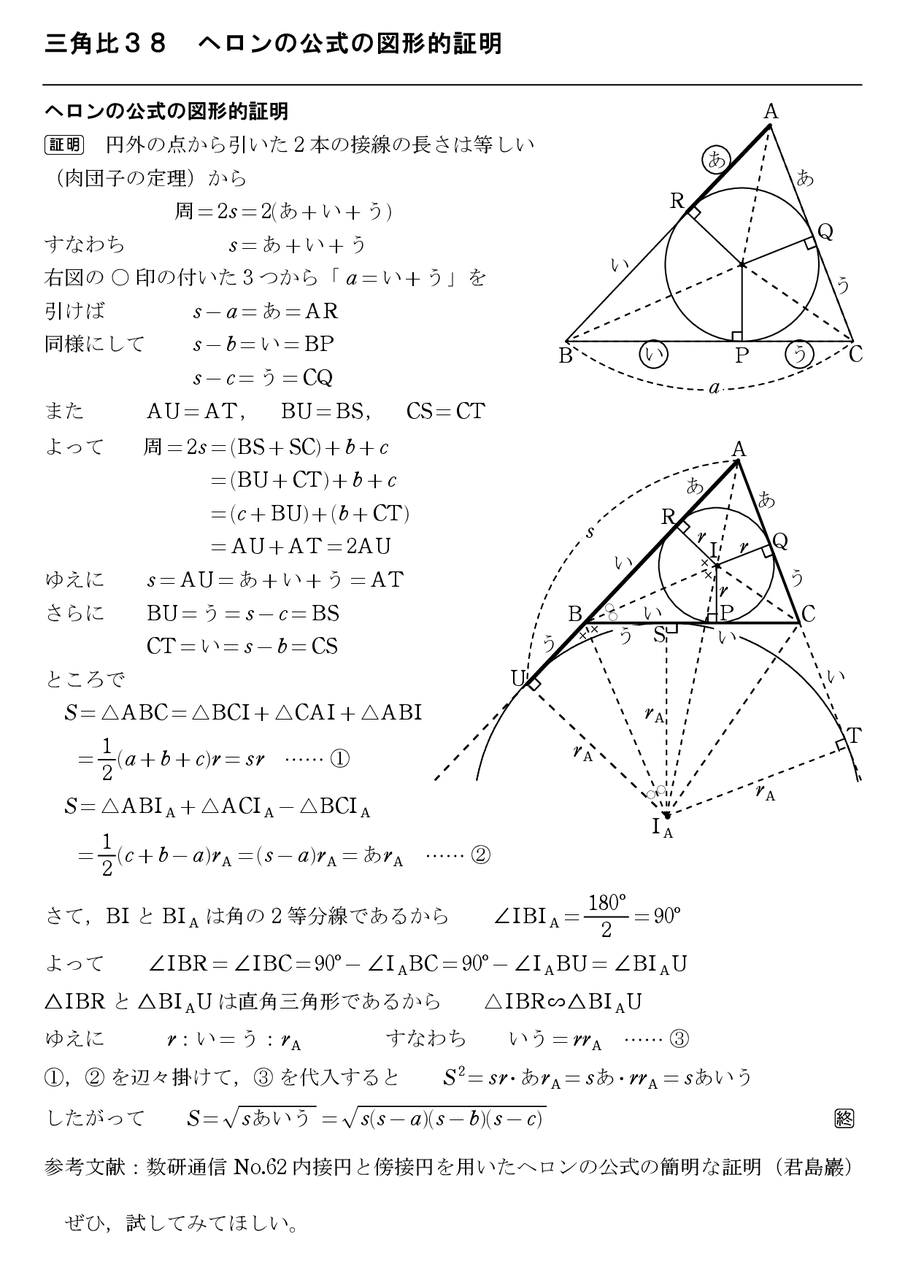



ヘロン の 公式 証明
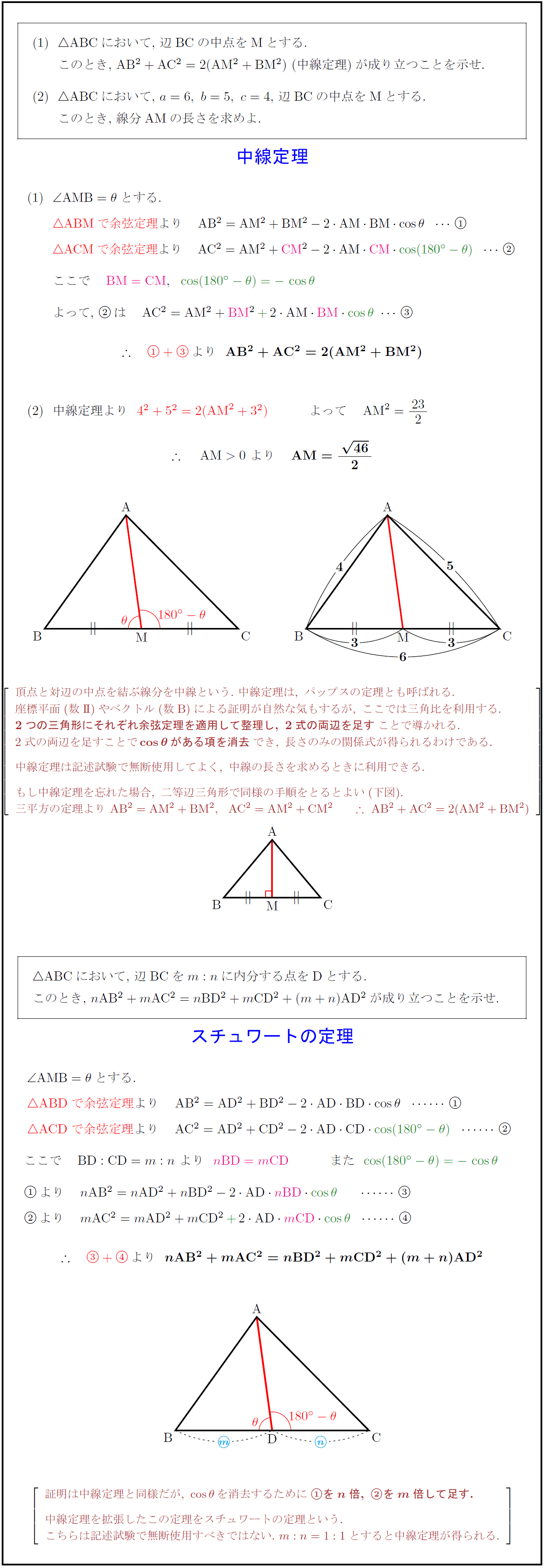



高校数学 中線定理 パップスの定理 とスチュワートの定理の三角比による証明 受験の月



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



外接円とは 半径の公式や求め方 性質 書き方 受験辞典



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




三角比 怜悧玲瓏 高校数学を天空から俯瞰する



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
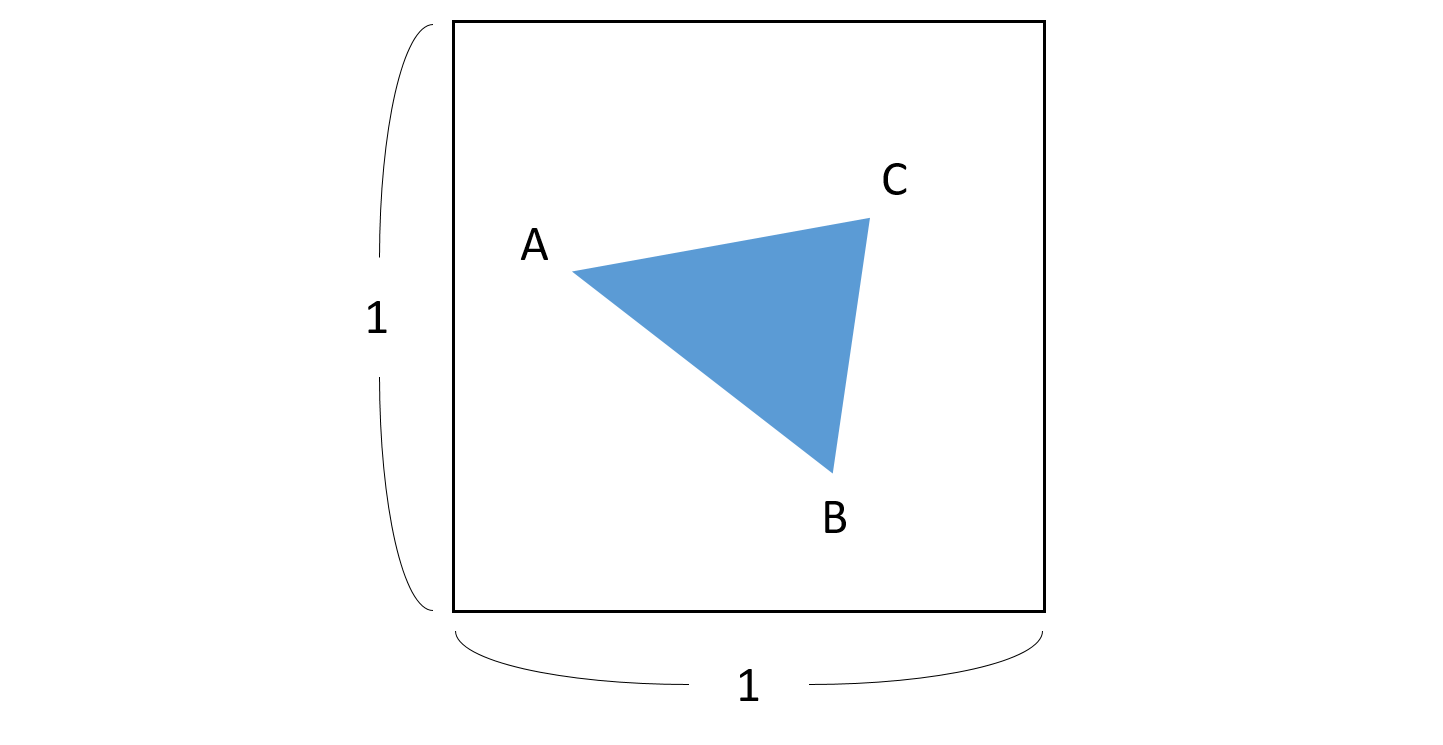



正方形の中にある三角形の面積の平均 Musyokutoumei




トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ




17年08月 東大合格コム
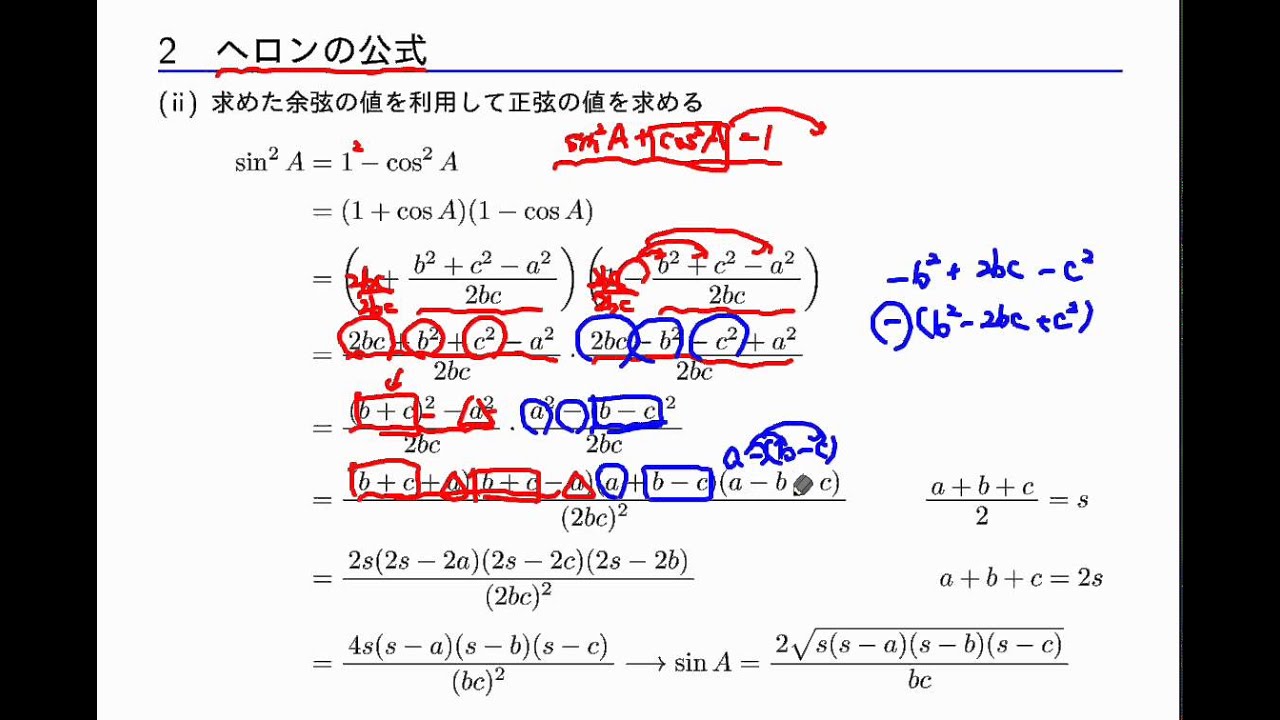



ヘロンの公式 まなびの学園




三角比の添削 追記9月14日 Matsu Math Note




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張



No comments:
Post a Comment